Last updated on September 4th, 2023 at 09:49 pm
Here, We will learn about algorithms analysis, types of analysis – priori and posterior analysis, how to two compare algorithms, algorithm complexity – time complexity and space complexity, runtime analysis of algorithms.
Algorithms Analysis:
Algorithms Analysis help us to determine which algorithms are more efficient.
The goal of algorithms analysis is to compare algorithms in terms of running time and space consumed.
Efficiency of an algorithm can be analyzed at two different stages, before implementation and after implementation. They are following :
Priori Analysis :
This is a theoretical analysis of an algorithm. Efficiency of an algorithm is measured by assuming that all other factors, for example, processor speed, are constant.
Posterior Analysis :
This is an empirical analysis of an algorithm. The selected algorithm is implemented using programming language and then executed on target computer machine. In this analysis, actual statistics like running time and space required, are collected.
Running time of an operation can be defined as number of computer instructions executed per operation.
Types of Analysis in Algorithm
To analyze the given algorithms, we need to know with which inputs the algorithms takes less time (performing well) and with which inputs the algorithms takes a long time.
There are three types of analysis:
- Worst Case: Defines the input for which the algorithm takes a long time (slowest time to complete).
- Best Case: Defines the input for which the algorithm takes the least time (fastest time to complete).
- Average Case: Provides a prediction about running time of the algorithms with random inputs.
How to Compare two Algorithms?
To compare algorithms, few objective are :
- Execution times ? execution times are specific to a particular computer.
- Number of statements executed ? the number of statements varies with the programming language as well as the style of the individual programmer.
- Ideal solution ? running time of a given algorithm as a function of the input size n (i.e., f(n))
Algorithm Complexity
Efficiency of an algorithm is depend upon time and space used by the algorithm.
Space Complexity – How much memory is used?
Time Complexity – How many primitive operations are executed?
Space Complexity :
Space Complexity of an algorithm represents the amount of memory space required by algorithm in its life cycle.
Space complexity S(P) of any algorithm P is S(P) = C + SP(I) where C is the fixed part and S(I) is the variable part which depends on instance characteristics I.
Time Complexity :
Time Complexity of an algorithm represents the amount of time required by the algorithm to run to completion.
Computational Time is T(n) = c*n where c is the time taken for addition of 2 bits and n is the number of steps.
Complexity of Common Operations :
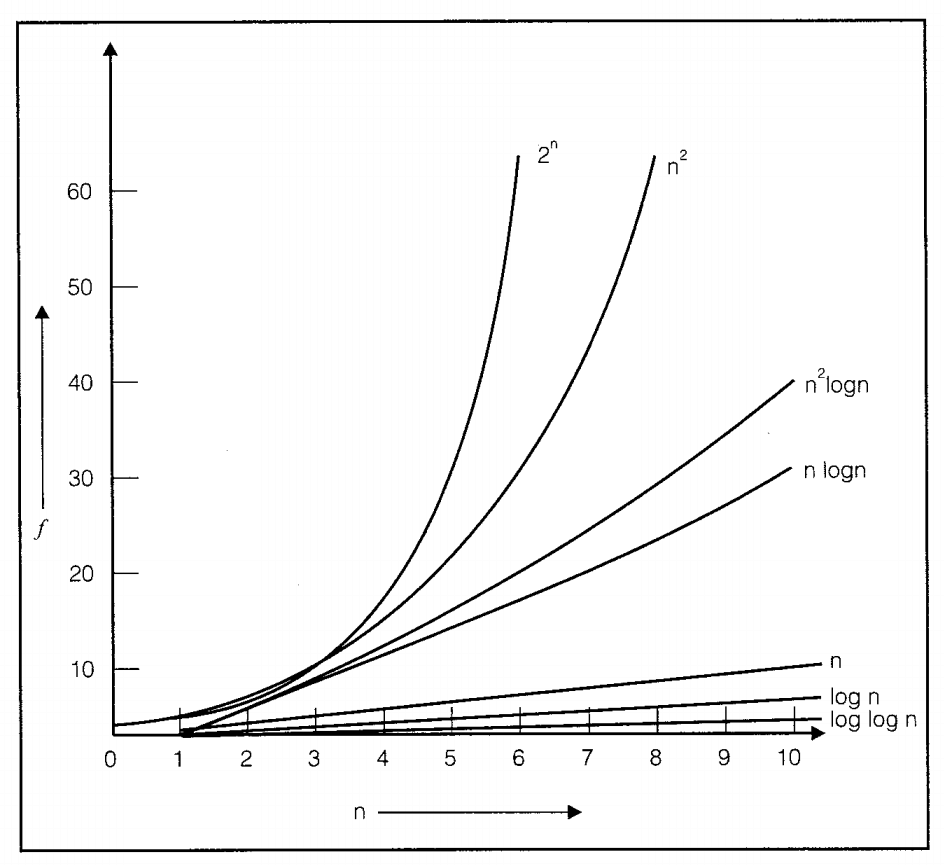
| Complexity | Operation |
| O(1) | Running a statement |
| O(1) | Value look-up on an array, object, variable |
| O(log n) | Loop that cuts problem in half every iteration |
| O(n) | Looping through the values of an array |
| O(n2) | Double nested loops |
| O(n3) | Triple nested loops |
Runtime Analysis of algorithms
Running time analysis is the process of determining how processing time increases as the size of the input elements increases.
Some common types of inputs are :
- Size of an array
- Polynomial degree
- Number of elements in a matrix
- Number of bits in the binary representation of the input
- Vertices and edges in a graph.
Related:
Want to Contribute:-
If you like “To The Innovation” and want to contribute, you can mail your articles to 📧 contribute@totheinnovation.com. See your articles on the main page and help other coders.😎