Heap Sort

Here, We will discuss about Heap Sort in C, their algorithm, implementation code in C, time and space complexity, and their applications.

What is Heap Sort?

Heap Sort is a comparison-based sorting algorithm. This sorting algorithm has more favorable worst-case O(n log n) runtime.

Heap Sort is an in-place algorithm but is not a stable sort.

Heaps can be used in sorting an array. In max-heaps, the maximum element will always be at the root.

Heap Sort uses this property of heap to sort the array.

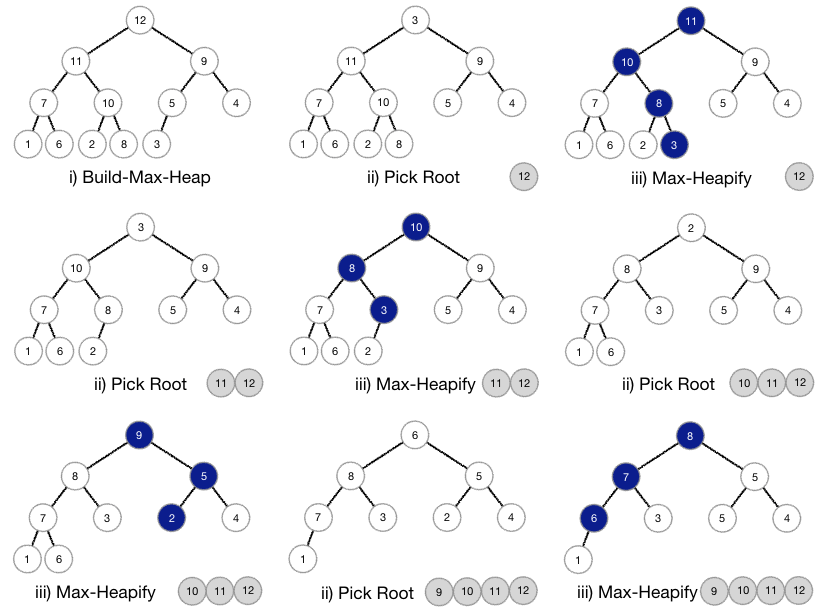
Heap Sort Algorithm

1. The tree satisfies Max-Heap property, then the largest element is stored at the root node.
2. Swap: Remove the root element and put at the end of the array (n^th position). Put the last item of the tree(heap) at the vacant place.
3. Remove: Reduce the size of the heap by 1.
4. Heapify: Heapify the root element again so that we have the largest element at root.
5. The process is repeated until all items of the list are sorted.

Implementation of Radix Sort

Program Code in C

#include<stdio.h>

//function to swap the position of two elements
void swap(int *a, int *b)
{
  int temp = *a;
  *a = *b;
  *b = temp;
}

void heapify(int arr[], int n, int i)
{
  //find largest among root, left and right child
  int largest = i;
  int left = 2*i+1;
  int right = 2*i+2;

  if(left<n && arr[left]>arr[largest])
    largest = left;

  if(right<n && arr[right]>arr[largest])
    largest = right;

  //swap and continue heapifying if root is not largest
  if(largest != i)
  {
    swap(&arr[i], &arr[largest]);
    heapify(arr, n, largest);
  }
}

//main function to do heap sort
void heapsort(int arr[], int n)
{
  //build max-heap
  for(int i=n/2-1; i>=0; i--)
    heapify(arr, n, i);

  //heap sort
  for(int i=n-1; i>=0; i--)
  {
    swap(&arr[0], &arr[i]);

    //heapify root element to get highest element at root again
    heapify(arr, i, 0);
  }
}

//print an array
void printarray(int arr[], int n)
{
  for(int i=0; i<n; i++)
    printf("%d ", arr[i]);
  printf("\n");
}

//Driver code
int main()
{
  int data[] = {8, 4, 7, 1, 3, 5};
  int n = sizeof(data)/sizeof(data[0]);
  heapsort(data, n);
  
  printf("Sorted array : ");
  printarray(data, n);
}Code language: C++ (cpp)

Output

Sorted array : 1 3 4 5 7 8Code language: PHP (php)

Time and Space Complexity of Radix Sort

Time Complexity
Worst Case	O(n log n)
Best Case	O(n log n)
Average Case	O(n log n)
Space Complexity
Worst Case	O(1)

Applications of Radix Sort

Heap Sort is used when

1. Systems concerned with security and embedded systems such as Linux Kernel.
2. Want to extract smallest or largest from list of items without sorting the list

Related:

---

Want to Contribute:-

If you like “To The Innovation” and want to contribute, you can mail your articles to 📧 contribute@totheinnovation.com. See your articles on the main page and help other coders.😎