What is the Quick Sort Algorithm and how it works?

Last updated on January 31st, 2025 at 09:32 pm

This article explores the Quick Sort Algorithm, how it works, its recurrence relation, and its implementation in C++.

1. What is the Quick Sort Algorithm?

The Quick Sort Algorithm is one of the famous comparison-based sorting algorithms based on the divide-and-conquer algorithmic technique.

Quick Sort Algorithm uses a recursive approach to sort an array of elements. It works by selecting a pivot element, partitioning the array around the pivot, and recursively sorting the sub-arrays. This process continues until the entire array is sorted.

The algorithm starts by picking an item, called a pivot, and moving all smaller items before it, while all greater elements after it. Selecting a random pivot in an array results in an improved complexity in most of the cases.

It reduces the space complexity and removes the use of the auxiliary array that is used in merge sort.

2. How Does Quick Sort Algorithm Work?

The Quick Sort Algorithm works in the following steps:

1. Select a Pivot: Choose an element from the array as the pivot.
2. Partition: Rearrange the array such that all elements less than the pivot are on the left, and all elements greater than the pivot are on the right.
3. Recursion: Recursively apply the Quick Sort Algorithm to the sub-arrays on the left and right of the pivot.

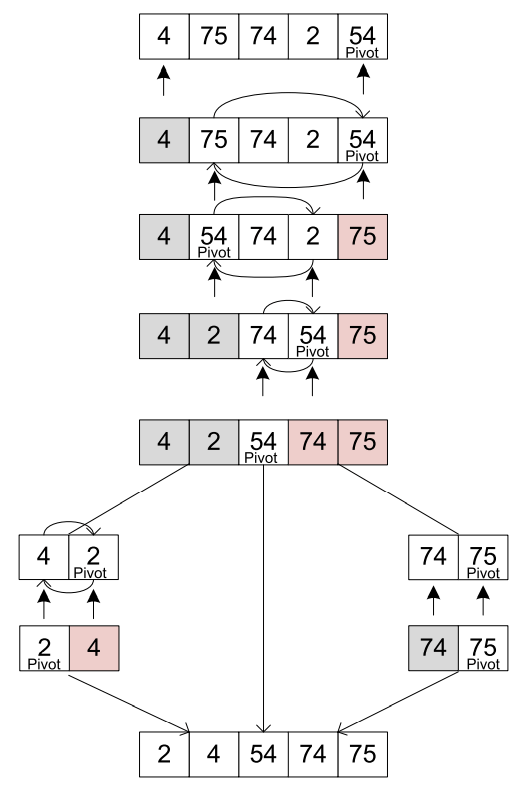
3. Randomised Quick Sort

To avoid worst-case scenarios, a variation of the Quick Sort Algorithm called Randomised Quick Sort is used. It improves its performance by randomly selecting the pivot element.

This randomization helps in avoiding the worst-case time complexity of O(n^2), which occurs when the smallest or largest element is always chosen as the pivot. By randomizing the pivot, the algorithm achieves an average time complexity of O(n log n).

4. Quick Sort Recurrence Relation

4.1 Recurrence Relation in Worst Case

The worst case of quick sort occurs when the pivot we picked turns out to be the least element of the array to be sorted, in every step (i.e. in every recursive call).

A similar situation will also occur if the pivot happens to be the largest element of the array to be sorted.

Then Recurrence Relation of Quick Sort in the worst case is

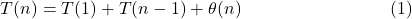
4.2 Recurrence Relation in Best Case

The best case of quick sort occurs when the pivot we picked happens to divide the array into two almost equal parts, in every step.

Thus, we have k = n/2 and n − k = n/2 for the original array of size n.

Then Recurrence Relation of Quick Sort in the best case is

5. Quick Sort Pseudo Code

Simple pseudo code for the Quick Sort Algorithm:

function quickSort(arr, low, high)
    if low < high
        pi = partition(arr, low, high)
        quickSort(arr, low, pi - 1)
        quickSort(arr, pi + 1, high)

function partition(arr, low, high)
    pivot = arr[high]
    i = low - 1
    for j = low to high - 1
        if arr[j] < pivot
            i = i + 1
            swap arr[i] and arr[j]
    swap arr[i + 1] and arr[high]
    return i + 1

6. Implementing Quick Sort in CPP

Basic implementation of Quick Sort in C++:

#include <iostream>
using namespace std;

void swap(int* a, int* b) {
    int t = *a;
    *a = *b;
    *b = t;
}

int partition(int arr[], int low, int high) {
    int pivot = arr[high];
    int i = (low - 1);
    for (int j = low; j <= high - 1; j++) {
        if (arr[j] < pivot) {
            i++;
            swap(&arr[i], &arr[j]);
        }
    }
    swap(&arr[i + 1], &arr[high]);
    return (i + 1);
}

void quickSort(int arr[], int low, int high) {
    if (low < high) {
        int pi = partition(arr, low, high);
        quickSort(arr, low, pi - 1);
        quickSort(arr, pi + 1, high);
    }
}

int main() {
    int arr[] = {10, 7, 8, 9, 1, 5};
    int n = sizeof(arr) / sizeof(arr[0]);
    quickSort(arr, 0, n - 1);
    cout << "Sorted array: ";
    for (int i = 0; i < n; i++)
        cout << arr[i] << " ";
    return 0;
}

7. Quick Sort vs Merge Sort

Quick Sort is generally faster for smaller datasets and has better cache performance due to its in-place sorting. However, Merge Sort is stable and guarantees O(n log n) time complexity, making it preferable for larger datasets or when stability is required.

8. Advantages of Quick Sort

1. Efficiency: Quick Sort is very efficient for large datasets. It has an average time complexity of O(n log n)
2. In-place Sorting: It requires only a small, constant amount of additional storage space.
3. Cache Performance: It has excellent cache performance due to its in-place partitioning.

9. Disadvantages of Quick Sort

1. Worst-case Complexity: The worst-case time complexity is O(n²), which can occur if the pivot selection is poor.
2. Stability: Quick sort is not a stable sort. Equal elements might not preserve their relative order.

10. Time and Space Complexity of Quick Sort

Time Complexity
Worst Case	O(n2)
Best Case	O(n log n)
Average Case	O(n log n)
Space Complexity
Worst Case	O(1)

11. Applications of Quick Sort

Quick Sort is implemented when

• space complexity matters
• the programming language is good for recursion
• time complexity matters

FAQs