Insertion Sort Pseudocode Count Steps

Last updated on January 5th, 2025 at 01:11 am

This article will explore the insertion sort, how it works, and Insertion Sort Pseudocode Count Steps comparisons.

1. What is the Insertion Sort Algorithm?

Insertion Sort is a simple and efficient comparison sort. It is in-place Sorting. The Insertion Sort inserts each element into its proper position. It chooses one element, inserts it into its position, and shifts the rest of the list by one location. This process is repeated until no input element remains.

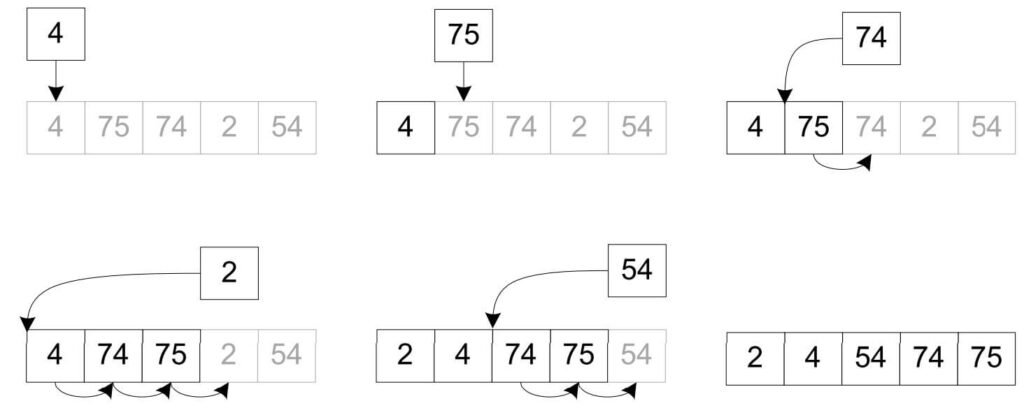
2. How Does Insertion Sort Algorithm Work?

The insertion sort algorithm works by iterating through the array one element at a time, inserting each element into its correct position within the sorted region. The algorithm consists of the following steps:

1. Start with the second element: Assume the first element is already sorted.
2. Compare the current element with the elements in the sorted portion.
3. Shift elements in the sorted portion to the right to make space for the current element.
4. Insert the current element into its correct position.
5. Repeat the process for all elements in the array.

3. Insertion Sort Pseudocode Count Steps

3.1 Insertion Sort Pseudocode

for i = 1 to length(A) - 1
    key = A[i]
    j = i - 1
    while j >= 0 and A[j] > key
        A[j + 1] = A[j]
        j = j - 1
    A[j + 1] = key

3.2 Counting Steps and Comparisons

To count the steps in insertion sort, you need to consider the number of comparisons and shifts. The worst-case scenario occurs when the array is sorted in reverse order, leading to the maximum number of comparisons and shifts.

• Comparisons: In the worst case, the number of comparisons is approximately n(n−1)/2.
• Shifts: Similarly, the number of shifts is also approximately n(n−1)/2.

4. Recurrence Relation of Insertion Sort

The Recurrence Relation for Insertion Sort is

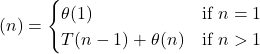
5. Implementing Insertion Sort in CPP

Here’s a simple implementation of insertion sort in C++ (CPP):

#include <iostream>
using namespace std;

void insertionSort(int arr[], int n) {
    for (int i = 1; i < n; i++) {
        int key = arr[i];
        int j = i - 1;
        while (j >= 0 && arr[j] > key) {
            arr[j + 1] = arr[j];
            j = j - 1;
        }
        arr[j + 1] = key;
    }
}

int main() {
    int arr[] = {12, 11, 13, 5, 6};
    int n = sizeof(arr) / sizeof(arr[0]);
    insertionSort(arr, n);
    for (int i = 0; i < n; i++)
        cout << arr[i] << " ";
    return 0;
}

6. How to Count Comparisons in Insertion Sort

Counting comparisons in insertion sort involves tracking each time an element is compared to another. This can be done by adding a counter within the while loop of the pseudocode. Each time the condition A[j] > key is checked, increment the counter.

comparisons = 0
for i = 1 to n-1
  key = arr[i]
  j = i-1
  while j >= 0 and arr[j] > key
    comparisons = comparisons + 1
    arr[j+1] = arr[j]
    j = j-1
  arr[j+1] = key

7. Is Insertion Sort Recursive?

No, the insertion sort algorithm is not recursive. It uses a simple iterative approach to sort the array, making it efficient and easy to implement.

8. Advantages of Insertion Sort

1. Simple implementation and easy to understand.
2. Efficient for small datasets or nearly sorted data.
3. In-place sorting algorithm, meaning it doesn’t require additional memory.

9. Disadvantages of Insertion Sort

1. Inefficient for large data sets. Its average and worst-case time complexity is O(n²), where n is the number of elements.
2. Not suitable for data sets with a large number of inversions.

10. Time and Space Complexity of Insertion Sort

Time Complexity
Worst Case	O(n2)
Best Case	O(n)
Average Case	O(n2)
Space Complexity
Worst Case	O(n2) total O(1) auxiliary

FAQs