Last updated on January 31st, 2025 at 09:18 pm
This article explores the Bubble Sort Algorithms, their pseudocode, problems like Can Bubble Sorter Used in Alphabetical Order?, and implementations in various programming languages like C++ and C.
Table of Contents
1. What is Bubble Sort Algorithm?
Bubble Sort Algorithm is a comparison-based algorithm. It uses a simple and intuitive approach to sort elements in a list. It works by repeatedly iterating through the list, comparing adjacent elements, and swapping them if they are in the wrong order.
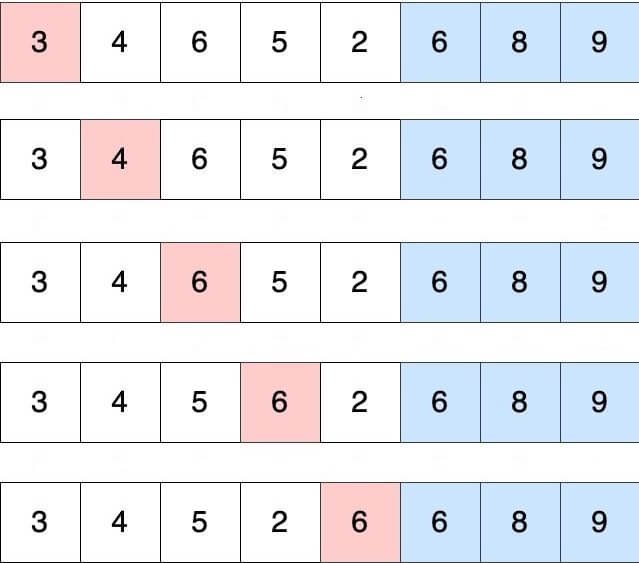
Bubble Sort is simple but having high time complexity
1.1 Example of Bubble Sort
Sort the given elements (7, 5, 2, 4, 3 and 9) by using bubble sort. After the first pass, we get 7, 5, 2, 4, 3, 9 5, 7, 2, 4, 3, 9 5, 2, 7, 4, 3, 9 5, 2, 4, 7, 3, 9 5, 2, 4, 3, 7, 9 After the first pass, the first largest element (9) is on the top of array. So we have 5, 2, 4, 3, 7, 9 After the second pass, we get 2, 4, 3, 5, 7, 9 After the third pass, we get 2, 3, 4, 5, 7, 9 After the fourth pass, we get 2, 3, 4, 5, 7, 9 After the fifth pass, we get 2, 3, 4, 5, 7, 9 The sorted list is 2, 3, 4, 5, 7, 9
2. Bubble Sort Pseudocode
Procedure BubbleSort(arr)
n = length(arr)
for i = 0 to n-1
for j = 0 to n-i-1
if arr[j] > arr[j+1]
swap arr[j] and arr[j+1]
return arr
3. How Does Bubble Sort Work?
The bubble sort algorithm works by repeatedly iterating through the list and comparing adjacent elements. If the elements are in the wrong order, they are swapped. This process is repeated until the list is sorted.
4. C++ Bubble Sort Implementation
Here is an example implementation of bubble sort in C++:
#include <iostream>
using namespace std;
void bubbleSort(int arr[], int n) {
for (int i = 0; i < n-1; i++) {
for (int j = 0; j < n-i-1; j++) {
if (arr[j] > arr[j+1]) {
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
}
int main() {
int arr[] = {64, 34, 25, 12, 22, 11, 90};
int n = sizeof(arr)/sizeof(arr[0]);
bubbleSort(arr, n);
cout << "Sorted array: ";
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
return 0;
}
5. Can Bubble Sort Be Used for Descending Order?
Yes, Bubble Sort can be used to sort data in descending order. By simply modifying the comparison operator in the algorithm, you can reverse the sorting order. To do this, you can simply modify the comparison operator in the algorithm < instead of >.
6. C Program to Bubble Sort
Here is an example implementation of bubble sort in C:
#include <stdio.h>
void bubbleSort(int arr[], int n) {
for (int i = 0; i < n-1; i++) {
for (int j = 0; j < n-i-1; j++) {
if (arr[j] > arr[j+1]) {
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
}
int main() {
int arr[] = {64, 34, 25, 12, 22, 11, 90};
int n = sizeof(arr)/sizeof(arr[0]);
bubbleSort(arr, n);
printf("Sorted array: ");
for (int i = 0; i < n; i++) {
printf("%d ", arr[i]);
}
return 0;
}
7. Can Bubble Sorter Used in Alphabetical Order?
Yes, bubble sort can be used to sort strings in alphabetical order. To do this, you can modify the comparison operator in the algorithm to compare the ASCII values of the characters.
8. Advantages of Bubble Sort
- Bubble Sort is straightforward to understand and implement.
- It requires only a constant amount of extra memory space.
- It preserves the relative order of equal elements.
- It is suitable for small datasets.
9. Disadvantages of Bubble Sort
- Bubble Sort has poor time complexity, making it inefficient for large datasets.
- It has a time complexity of O(n2), making it inefficient for large datasets.
- It does not adapt to the data in any way. Even if the array is sorted, it will still perform O(n2) comparisons.
10. Time and Space Complexity of Bubble Sort
| Time Complexity | |
| Worst Case | O(n2) |
| Best Case | O(n) |
| Average Case | O(n2) |
| Space Complexity | |
| Worst Case | O(1) |
FAQs
1. Is Bubble Sort stable?
Yes, Bubble Sort is a stable sorting algorithm. It maintains the relative order of equal elements in the sorted list.
2. Can Bubble Sort be optimized?
Yes, Bubble Sort can be optimized by adding a flag to detect if the list is already sorted, which can reduce the number of passes through the list.
3. Can bubble sort be used for sorting arrays of objects?
Yes, bubble sort can be used for sorting arrays of objects.
4. Is Bubble Sort efficient for large datasets?
No, Bubble Sort is not efficient for large datasets due to its high time complexity. For large datasets, more efficient algorithms like Quick Sort, Merge Sort, or Heap Sort are preferred.
5. Can Bubble Sort be used for linked lists?
Yes, Bubble Sort can be used for linked lists. However, it is not the most efficient algorithm for this data structure. More efficient algorithms for linked lists include Merge Sort and Insertion Sort.
6. How does Bubble Sort handle duplicate values?
Bubble Sort effectively handles duplicate values by ensuring that equal elements remain in their relative order. The algorithm compares and swaps adjacent elements, so duplicates will not affect the sorting process.
7. What is the time complexity of Bubble Sort?
The time complexity of Bubble Sort is O(n^2) in the worst and average cases, where n is the number of elements in the list. This makes it inefficient for large datasets.











