Last updated on January 31st, 2025 at 08:47 pm
his article will explore the Merge Sort Algorithm, including its pseudocode, recurrence relation, and practical implementations in C and C++.
Table of Contents
1. What is the Merge Sort Algorithm?
Merge Sort Algorithm is a divide-and-conquer algorithm. It divides the input array into two subarrays, calls itself for the two sub-arrays, and then merges the two sorted arrays.
Merge Sort is a stable sort. It is not an in-place sorting technique.
Merge sort is not preferable for smaller-size element array.
Merge sort is Quick Sort’s complement. This algorithm is used for sorting a linked list.
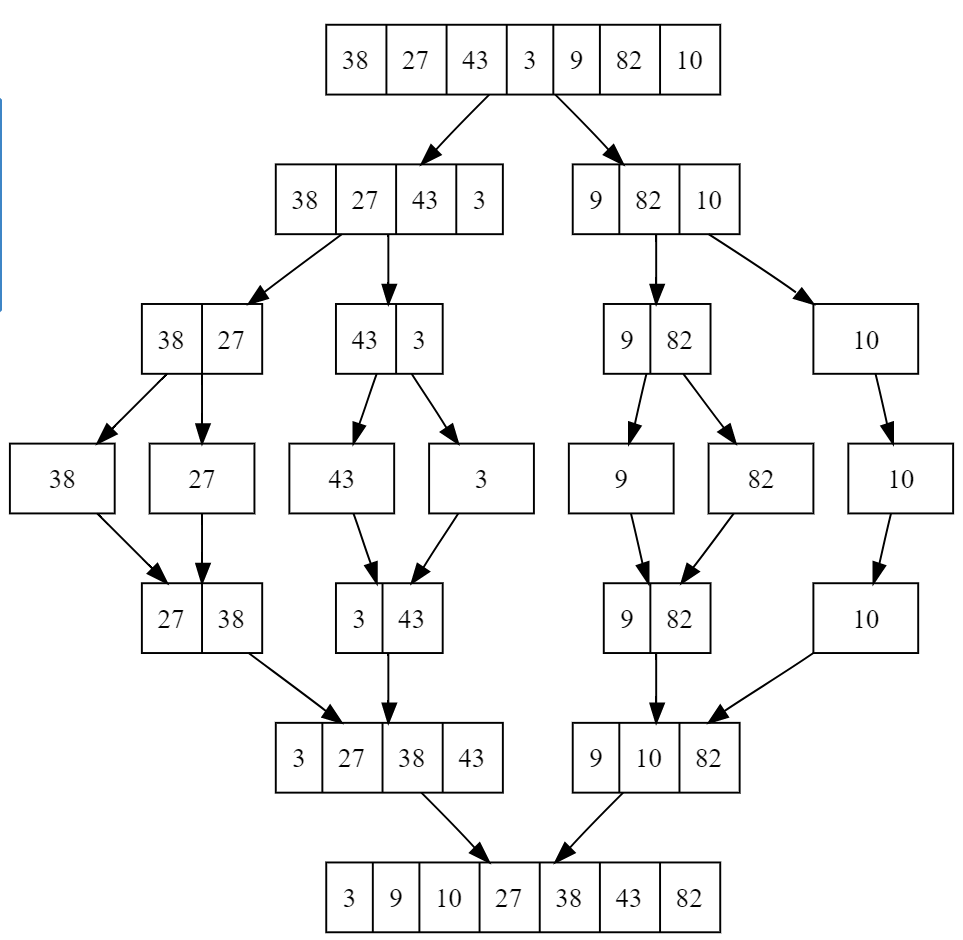
2. Merge Sort Pseudocode: A Step-by-Step Guide
To better understand the Merge Sort Algorithm, let’s explore its pseudocode:
function mergeSort(array)
if length(array) <= 1
return array
mid = length(array) / 2
left = mergeSort(array[0...mid])
right = mergeSort(array[mid+1...end])
return merge(left, right)
function merge(left, right)
result = []
while left and right are not empty
if left[0] <= right[0]
append left[0] to result
remove left[0] from left
else
append right[0] to result
remove right[0] from right
append remaining elements of left and right to result
return result
3. Merge Sort Recurrence Relation
The Recurrence Relation for Merge Sort is

This relation indicates that the algorithm divides the problem into two subproblems of size n/2 and requires linear time Θ(n) to merge the sublists.
The overall time complexity of the Merge Sort Algorithm is O(n log n), making it highly efficient for large datasets.
4. Implementing the Merge Sort Algorithm
4.1 C Program of Merge Sort
#include <stdio.h>
void merge(int arr[], int left, int mid, int right) {
int n1 = mid - left + 1;
int n2 = right - mid;
int L[n1], R[n2];
for (int i = 0; i < n1; i++)
L[i] = arr[left + i];
for (int j = 0; j < n2; j++)
R[j] = arr[mid + 1 + j];
int i = 0, j = 0, k = left;
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
} else {
arr[k] = R[j];
j++;
}
k++;
}
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
while (j < n2) {
arr[k] = R[j];
j++;
k++;
}
}
void mergeSort(int arr[], int left, int right) {
if (left < right) {
int mid = left + (right - left) / 2;
mergeSort(arr, left, mid);
mergeSort(arr, mid + 1, right);
merge(arr, left, mid, right);
}
}
int main() {
int arr[] = {12, 11, 13, 5, 6, 7};
int arr_size = sizeof(arr) / sizeof(arr[0]);
mergeSort(arr, 0, arr_size - 1);
printf("Sorted array: \n");
for (int i = 0; i < arr_size; i++)
printf("%d ", arr[i]);
return 0;
}
4.1.1 Explanation of Merge Sort line by line
- Splitting the array: Merge Sort starts by recursively dividing the array into halves until each sub-array contains only one element.
- Merging: Then it combines the sorted sub-arrays back together. It compares elements from both sub-arrays during the merge and arranges them in sorted order.
- Combining: This process continues until the entire array is sorted.
4.2 Merge Sort Algorithm in C++
#include <iostream>
#include <vector>
void merge(std::vector<int>& arr, int left, int mid, int right) {
int n1 = mid - left + 1;
int n2 = right - mid;
std::vector<int> L(n1), R(n2);
for (int i = 0; i < n1; i++)
L[i] = arr[left + i];
for (int j = 0; j < n2; j++)
R[j] = arr[mid + 1 + j];
int i = 0, j = 0, k = left;
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
} else {
arr[k] = R[j];
j++;
}
k++;
}
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
while (j < n2) {
arr[k] = R[j];
j++;
k++;
}
}
void mergeSort(std::vector<int>& arr, int left, int right) {
if (left < right) {
int mid = left + (right - left) / 2;
mergeSort(arr, left, mid);
mergeSort(arr, mid + 1, right);
merge(arr, left, mid, right);
}
}
int main() {
std::vector<int> arr = {12, 11, 13, 5, 6, 7};
mergeSort(arr, 0, arr.size() - 1);
std::cout << "Sorted array: \n";
for (int i = 0; i < arr.size(); i++)
std::cout << arr[i] << " ";
return 0;
}
5. Merge K Sorted Lists Using Merge Sort Algorithm
The Merge Sort Algorithm can be extended to merge k-sorted lists efficiently. This involves repeatedly merging pairs of lists until only one sorted list remains. This approach is particularly useful in scenarios involving large datasets distributed across multiple sources.
6. Advantages of Merge Sort Algorithm
- It guarantees a worst-case time complexity of O(n log n), where n is the number of elements.
- Stable sorting algorithm, meaning it preserves the relative order of equal elements.
- Performs well on large data sets and is efficient for sorting linked lists.
7. Disadvantages of Merge Sort Algorithm
- Requires additional memory space for the merging process, which can be a disadvantage for large arrays or in memory-constrained environments.
- It is slower than other sorting algorithms for small data sets or arrays that can fit entirely in memory.
8. Time and Space Complexity of Merge Sort Algorithm
| Time Complexity | |
| Worst Case | O(n log n) |
| Best Case | O(n log n) |
| Average Case | O(n log n) |
| Space Complexity | |
| Worst Case | O(n) |
9. Applications of Merge Sort Algorithm
- Merge sort is useful for sorting linked lists in O(n log n) time. Other (n log n) algorithms such as heap sort and quick sort (average case n log n) cannot be applied to linked lists.
- It is used in the inversion count problem.
- It is used in external sorting.
FAQs
1. What is the Merge Sort Algorithm used for?
The Merge Sort Algorithm is used for sorting elements in a list or array. It is particularly effective for large datasets due to its O(n log n) time complexity.
2. How does the Merge Sort Algorithm work?
The Merge Sort Algorithm works by dividing the list into smaller sublists, sorting each sublist, and then merging them back together in a sorted order.
3. What are the advantages of using the Merge Sort Algorithm?
The Merge Sort Algorithm is stable, works well with large datasets, and is suitable for external sorting.
4. Why is the Merge Sort Algorithm considered stable?
The Merge Sort Algorithm is considered stable because it maintains the relative order of equal elements in the input list.
5. Can the Merge Sort Algorithm be used for linked lists?
Yes, the Merge Sort Algorithm is particularly well-suited for linked lists because it does not require random access to elements, which is a limitation of linked lists.
6. How does Merge Sort handle large datasets?
Merge Sort’s divide-and-conquer approach makes it efficient for large datasets. It ensures that the sorting process is consistent, regardless of the data size.
7. What is the time complexity of the Merge Sort Algorithm?
The time complexity of the Merge Sort Algorithm is O(n log n), making it efficient for large datasets.











