Last updated on January 31st, 2025 at 09:40 pm
This article explores asymptotic notation cheat sheet, algorithm asymptotic analysis, as well as the types of notation: big-o notation, omega notation, theta notation, and asymptotic growth rate notation.
Table of Contents
1. What is Algorithm Asymptotic Analysis?
Asymptotic Analysis of an algorithm refers to computing the running time of any operation in mathematical units of computation. It is not perfect, but best way available for analyzing algorithms.
To analyze the asymptotic complexity of an algorithm, follow these steps:
- Identify the input size: Determine the size of the input that affects the algorithm’s performance.
- Count the operations: Count the number of operations performed by the algorithm.
- Express the complexity: Express the complexity as a function of the input size using Big O, Big Ω, or Big Θ notation.
Asymptotic Analysis can be performed for different scenarios:
- Best-Case Scenario: The algorithm performs optimally, and the growth rate is the lowest.
- Average-Case Scenario: The algorithm performs averagely, and the growth rate is moderate.
- Worst-Case scenario: The algorithm performs poorly, and the growth rate is the highest.
2. What is Asymptotic Notation?
Asymptotic Notation is a mathematical tool used to describe the behavior of algorithms as the input size grows. It provides a way to express the upper, lower, and tight bounds of an algorithm’s running time or space requirements.
It is a standardized way of measuring how much memory an algorithm uses or how long it runs for the given input.
The following commonly used asymptotic notation is:
- Big-O Notation
- Omega-Ω Notation
- Theta-Θ Notation
- Little o Notation (o)
- Little omega Notation (ω)
2.1 Big O Notation (O)
Big O Notation (O) represents the upper bound of an algorithm’s growth rate. It is used to describe the worst-case scenario.
Big-O of g(n), written as f(n) = O(g(n))
Example: O(n^2) indicates that the algorithm’s performance will not exceed n^2 operations.

In the worst-case analysis, we calculate the upper bound on the running time of an algorithm.
2.2 Omega Notation (Ω)
Omega Notation (Ω) represents the lower bound of an algorithm’s growth rate. It is used to describe the best-case scenario.
Big-Omega of g(n), written as f(n) = Ω(g(n))
Example: Ω(n) suggests that the algorithm will take at least n operations.

In the best-case analysis, we calculate the lower bound on the running time of an algorithm.
2.3 Theta Notation (Θ)
Theta Notation (Θ) represents the tight bound of an algorithm’s growth rate. It is used when the upper and lower bounds are the same.
Big-Theta of g(n), written as f(n) = Θ(g(n))
Example: Θ(n log n) indicates that the algorithm’s performance is tightly bound to n log n operations.
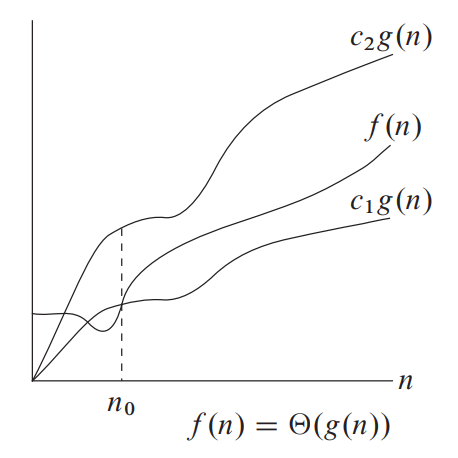
In average case analysis, we take all possible inputs and calculate computing time for all of its inputs.
Lower Bound <= Average Time <= Upper Bound
2.4 Little o Notation (o)
Little o Notation (o) describes an upper bound that is not tight. It is used to show that an algorithm’s growth rate is strictly less than another.
Example: o(n^2) implies the algorithm grows slower than n^2.
2.5 Little omega Notation (ω)
Little omega Notation (ω) describes a lower bound that is not tight. It is used to show that an algorithm’s growth rate is strictly more than another.
Example: ω(n) suggests the algorithm grows faster than n.
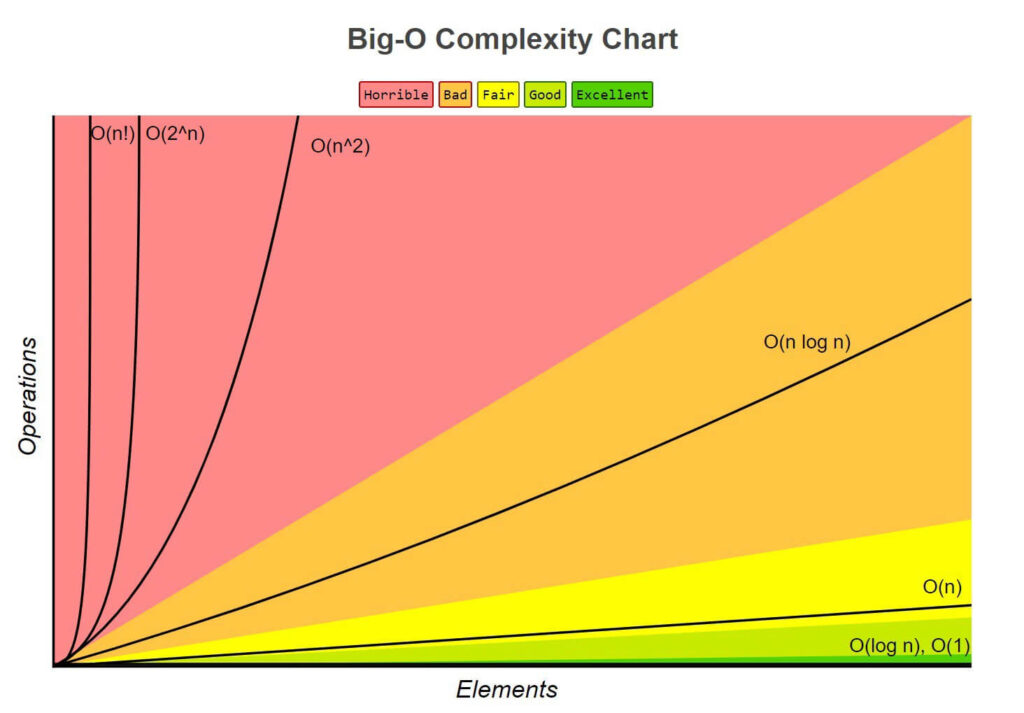
3. Asymptotic Growth Rate Notation – Growth Rate of Algorithm
Asymptotic Growth Rate Notation helps in comparing the efficiency of different algorithms. By analyzing the growth rate, developers can predict how an algorithm will perform as the input size increases, which is crucial for optimizing performance.
Growth Rate of Algorithm is the rate at which the running time increases as a function of input.
log(n!) < (log(n))!
log(log*n) < log*(log n)
n < (log n)log n
2n < n! < nn
4. Growth Rate of Algorithm: Why is it Important?
Understanding the growth rate of an algorithm is crucial because it helps:
- Predict performance: Predict the performance of an algorithm on large inputs.
- Compare algorithms: Compare the performance of different algorithms.
- Optimize algorithms: Optimize algorithms to improve their performance.
5. Asymptotic Notation Cheat Sheet
Here’s a comprehensive cheat sheet to help you quickly identify the growth rate of an algorithm:
| Time Complexity | Name | Example |
| O(1) | Constant | Adding an element to the front of a linked list, Accessing an array by index |
| O(log n) | Logarithmic | Finding an element in a sorted array |
| O(n) | Linear | Finding an element in an array |
| O(n log n) | Linear Logarithmic | Merging two sorted arrays |
| O(n2) | Quadratic | Shortest path between two nodes in a graph, Bubble sort algorithm |
| O(n3) | Cubic | Matrix Multiplication |
| O(2n) | Exponential | The Tower of Hanoi, Recursive Fibonacci sequence |
FAQs
1. What is the purpose of Asymptotic Notation?
Asymptotic Notation is used to describe the efficiency of algorithms in terms of time and space complexity as the input size grows.
2. How do you determine the Growth Rate of Algorithm?
The Growth Rate of Algorithm is determined by analyzing the algorithm’s performance as the input size increases, using notations like Big O, Omega, and Theta.
3. Why is Big O Notation important in Algorithm Asymptotic Analysis?
Big O Notation is crucial because it provides a worst-case scenario, helping developers understand the maximum resources an algorithm might require.
4. Can Asymptotic Notation be used for space complexity analysis?
Yes, Asymptotic Notation can be applied to both time and space complexity to evaluate an algorithm’s efficiency.
5. What is the difference between Big O and Theta Notation?
Big O describes an upper bound, while Theta provides a tight bound, meaning the algorithm’s growth rate is both upper and lower bounded by the same function.
6. Can Asymptotic Notation be applied to all algorithms?
Yes, Asymptotic Notation is a universal tool applicable to any algorithm, offering a consistent method for performance evaluation.











