Last updated on January 31st, 2025 at 09:22 pm
This article explores Depth First Search, its recursive and iterative implementations, and its time complexity, and provides code examples in Python and JavaScript.
Table of Contents
1. What is Depth First Search?
Depth First Search (DPS) is a graph traversal algorithm that explores as far as possible along each branch before backtracking. It uses a stack-based approach, either explicitly (in iterative implementations) or implicitly (via recursion). DFS is particularly useful for tasks like detecting cycles, finding connected components, and solving puzzles like mazes.
Depth First Search (DFS) is a recursive algorithm that uses the idea of backtracking. It works similarly to the preorder traversal of the tree. This algorithm is similar to the standard algorithm for traversing binary trees. It uses the stack.
DFS is better choice if the solution is at maximum depth.
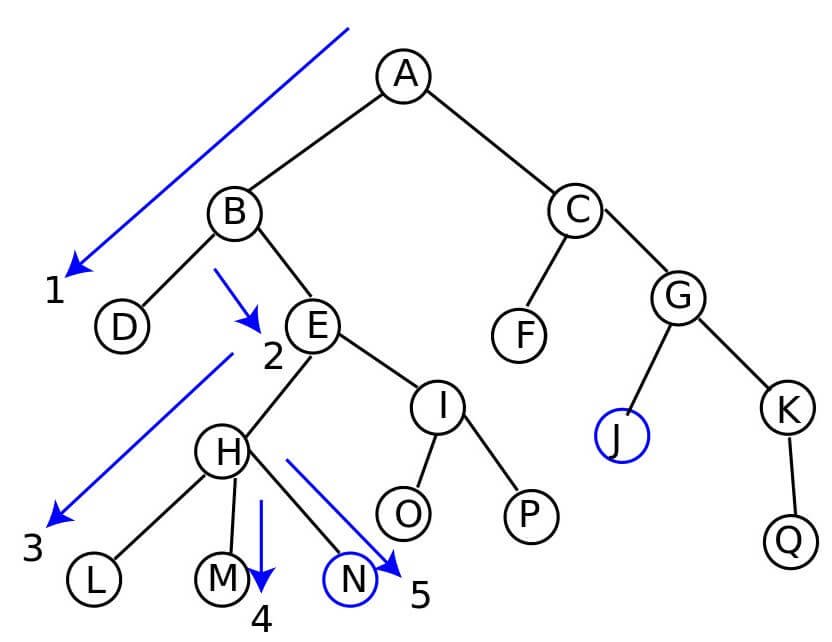
2. Recursive Depth First Search: How It Works
Recursive Depth First Search is the most intuitive way to implement DFS. It leverages the call stack to keep track of visited nodes and backtrack when necessary. Here’s a step-by-step breakdown of how Recursive Depth First Search operates:
- Start at the root node (or any arbitrary node in a graph).
- Mark the current node as visited.
- Recursively visit all unvisited neighbors of the current node.
- Backtrack when no unvisited neighbors remain.
def dfs_recursive(graph, node, visited):
if node not in visited:
visited.add(node)
print(node) # Process the node
for neighbor in graph[node]:
dfs_recursive(graph, neighbor, visited)
# Example
graph = {
'A': ['B', 'C'],
'B': ['D', 'E'],
'C': ['F'],
'D': [],
'E': [],
'F': []
}
visited = set()
dfs_recursive(graph, 'A', visited)
3. Iterative Depth First Search: A Stack-Based Approach
Iterative Depth First Search eliminates the need for recursion by explicitly using a stack to manage the traversal process. This approach is particularly useful in environments where recursion depth is limited or when you want more control over the traversal.
def dfs_iterative(graph, start):
visited = set()
stack = [start]
while stack:
node = stack.pop()
if node not in visited:
visited.add(node)
print(node) # Process the node
stack.extend(reversed(graph[node])) # Add neighbors to stack
# Example
graph = {
'A': ['B', 'C'],
'B': ['D', 'E'],
'C': ['F'],
'D': [],
'E': [],
'F': []
}
dfs_iterative(graph, 'A')
4. Breadth First Search in Different Programming Languages
4.1 Depth First Search Python Code
Implementation of Depth First Search in Python using the recursive approach:
def dfs(graph, start):
visited = set()
def dfs_helper(node):
visited.add(node)
for neighbor in graph[node]:
if neighbor not in visited:
dfs_helper(neighbor)
dfs_helper(start)
return visited
# Example
graph = {
'A': ['B', 'C'],
'B': ['A', 'D', 'E'],
'C': ['A', 'F'],
'D': ['B'],
'E': ['B', 'F'],
'F': ['C', 'E']
}
start_node = 'A'
visited_nodes = dfs(graph, start_node)
print(visited_nodes)
4.2 Depth First Search JavaScript
Implementation of Depth First Search in JavaScript using the iterative approach:
function dfs(graph, start) {
const visited = new Set();
const stack = [start];
while (stack.length > 0) {
const node = stack.pop();
visited.add(node);
for (const neighbor of graph[node]) {
if (!visited.has(neighbor)) {
stack.push(neighbor);
}
}
}
return visited;
}
// Example
const graph = {
'A': ['B', 'C'],
'B': ['A', 'D', 'E'],
'C': ['A', 'F'],
'D': ['B'],
'E': ['B', 'F'],
'F': ['C', 'E']
};
const startNode = 'A';
const visitedNodes = dfs(graph, startNode);
console.log(visitedNodes);
5. Time Complexity Depth First Search
The time complexity of Depth First Search depends on the structure of the graph. In the best case, when the graph is a tree, the time complexity is O(|V| + |E|), where |V| is the number of vertices and |E| is the number of edges. In the worst case, when the graph is a complete graph, the time complexity is O(|V| + |E|) as well. However, in the average case, the time complexity is O(|V| + |E| / 2), assuming a random graph structure.
5.1 Depth First Search Average Case Runtime
The average case runtime of Depth First Search is O(|V| + |E| / 2), assuming a random graph structure. This is because the algorithm visits each node and edge once, resulting in a linear time complexity.
5.2 Depth First Search Best Case Runtime
The best case runtime of Depth First Search is O(|V| + |E|), which occurs when the graph is a tree. In this case, the algorithm visits each node and edge once, resulting in a linear time complexity.
5.3 Depth First Search Worst Case Runtime
The worst case runtime of Depth First Search is O(|V| + |E|), which occurs when the graph is a complete graph. In this case, the algorithm visits each node and edge once, resulting in a linear time complexity.
6. Advantages of Depth First Search
- Depth-first search on a binary tree generally requires less memory than breadth-first search.
- It can be easily implemented with recursion.
7. Disadvantages of Depth First Search
- A DFS doesn’t find the shortest path to a node, while a breadth-first search does.
8. Applications of Depth First Search
- Topological sorting
- Finding strongly connected components
- Find articulation points (cut vertices) of the graph
- Solving puzzles such as mazes
| Applications | DFS | BFS |
| Spanning forest, connected components, paths, cycles | Yes | Yes |
| Shortest paths | – | Yes |
| Minimal use of memory space | Yes | – |
FAQs
1. What is Depth First Search used for?
Depth First Search is used for tasks like pathfinding, cycle detection, topological sorting, and finding connected components in graphs.
2. How does Recursive Depth First Search differ from Iterative Depth First Search?
Recursive Depth First Search uses the call stack for backtracking, while Iterative Depth First Search explicitly uses a stack data structure.
3. Can Depth First Search be used on weighted graphs?
Yes, but DFS does not account for edge weights. For shortest-path problems, algorithms like Dijkstra’s or A* are more suitable.
4. Is Depth First Search a complete algorithm?
No, Depth First Search is not a complete algorithm, meaning it may not always find a solution if one exists. This is because DFS can get stuck in an infinite loop if the graph contains cycles and no unvisited nodes.
5. What is the difference between Depth First Search and Breadth First Search?
Depth First Search (DFS) explores as far as possible along each branch before backtracking, while Breadth First Search (BFS) explores all nodes at a given depth before moving on to the next depth level.
6. Is Depth First Search guaranteed to find the shortest path?
No, Depth First Search is not guaranteed to find the shortest path. It is possible for DFS to get stuck in an infinite loop if the graph contains cycles and no unvisited nodes.
7. What is the time complexity of Depth First Search?
The time complexity of Depth First Search is O(|V| + |E|) in the best case, O(|V| + |E| / 2) in the average case, and O(|V| + |E|) in the worst case, where |V| is the number of vertices and |E| is the number of edges.











