Last updated on January 31st, 2025 at 09:18 pm
This article thoroughly explores the Selection Sorting Algorithm, compares it with other sorting methods, and provides practical examples in Python and Java.
Table of Contents
1. What is Selection Sorting Algorithm?
The Selection Sorting Algorithm is an in-place comparison-based sorting algorithm that divides the array into two parts: the sorted portion and the unsorted portion. The algorithm iterates through the array, selecting the smallest or largest element from the unsorted portion and swapping it with the first element of the unsorted portion. This process continues until the entire array is sorted.
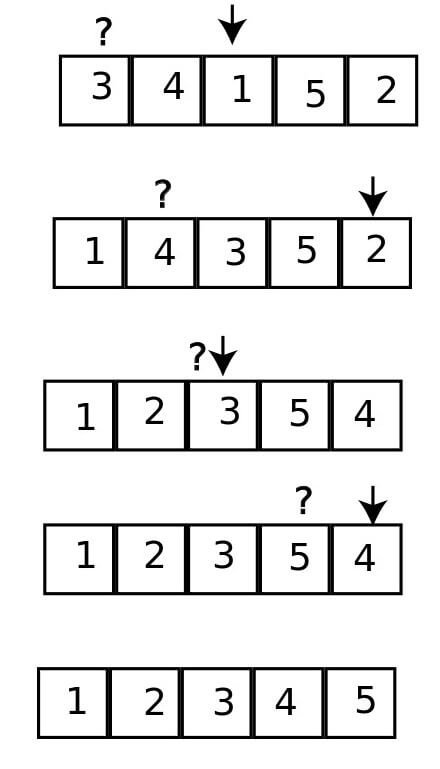
1.1 Example for Selection Sort
Sort the given elements (29, 64, 73, 34 and 20) by using selection sort. We have 29, 64, 73, 34, 20 After the first pass, we get 20, 64, 73, 34, 29 After the second pass, we get 20, 29, 73, 34, 64 After the third pass, we get 20, 29, 34, 73, 64 After the fourth pass, we get 20, 29, 34, 64, 73 After the fifth pass, we get 20, 29, 34, 64, 73 The sorted list is 20, 29, 34, 64, 73.
2. Selection Sort Pseudocode
Here is a step-by-step pseudocode for the Selection Sorting Algorithm:
- Initialize the array and its length.
- Iterate through the array from the first element to the second last element.
- For each iteration, assume the current element as the smallest or largest element.
- Iterate through the unsorted portion of the array to find the smallest or largest element.
- If a smaller or larger element is found, update the smallest or largest element index.
- Swap the smallest or largest element with the current element.
- Repeat steps 3-6 until the entire array is sorted.
procedure selectionSort(list, n)
for i = 0 to n-1
minIndex = i
for j = i+1 to n
if list[j] < list[minIndex]
minIndex = j
end if
end for
swap list[i] and list[minIndex]
end procedure
3. Insertion Sort vs Selection Sort
Both Insertion Sort and Selection Sort are simple sorting algorithms used for small datasets.
However, Insertion Sort is more efficient than Selection Sort for nearly sorted arrays, while Selection Sort is more efficient for arrays with a large number of duplicate elements.
4. Python Program for Selection Sort
Simple Python program for implementing the Selection Sorting Algorithm:
def selection_sort(arr):
for i in range(len(arr)):
min_index = i
for j in range(i + 1, len(arr)):
if arr[j] < arr[min_index]:
min_index = j
arr[i], arr[min_index] = arr[min_index], arr[i]
# Example
numbers = [64, 25, 12, 22, 11]
selection_sort(numbers)
print("Sorted array:", numbers)
5. Selection Sort Program in Java
Implementing Selection Sort Program in Java:
public class SelectionSort {
public static void selectionSort(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {
int minIndex = i;
for (int j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[minIndex]) {
minIndex = j;
}
}
int temp = arr[minIndex];
arr[minIndex] = arr[i];
arr[i] = temp;
}
}
public static void main(String[] args) {
int[] numbers = {64, 25, 12, 22, 11};
selectionSort(numbers);
System.out.println("Sorted array: " + Arrays.toString(numbers));
}
}
6. Advantages of Selection Sort
- Simple implementation.
- Doesn’t require extra space other than the array being sorted.
- Stable sorting algorithm
7. Disadvantages of Selection Sort
- Inefficient for large lists. Its complexity is O(n^2), where n is the number of elements.
- Not adaptive. The time complexity remains the same even if the list is partially sorted.
- Not suitable for real-time data
8. Time and Space Complexity of Selection Sort
| Time Complexity | |
| Worst Case | O(n2) |
| Best Case | O(n2) |
| Average Case | O(n2) |
| Space Complexity | |
| Worst Case | O(1) |
FAQs
1. Is Selection Sort stable?
No, Selection Sort is not a stable sorting algorithm. It can change the relative order of equal elements.
2. When should I use Selection Sort?
Selection Sort is best used for small datasets or when memory writes are costly, as it performs fewer swaps compared to other algorithms like Bubble Sort.
3. How does Selection Sort differ from Insertion Sort?
While both have a time complexity of O(n^2), Insertion Sort is generally more efficient for partially sorted arrays, whereas Selection Sort is simpler and performs fewer swaps.
4. Can the Selection Sorting Algorithm be used for real-time data?
No, the Selection Sorting Algorithm is not suitable for real-time data due to its high time complexity.
5. How does the Selection Sorting Algorithm compare to other sorting algorithms?
The Selection Sorting Algorithm is less efficient than other sorting algorithms like QuickSort, MergeSort, and HeapSort for large datasets. However, it is simple to implement and efficient for small datasets.
6. Can the Selection Sorting Algorithm be used for sorting linked lists?
Yes, the Selection Sorting Algorithm can be used for sorting linked lists. However, it may not be the most efficient algorithm for this purpose due to the overhead of traversing the linked list.
7. What is the time complexity of the Selection Sorting Algorithm?
The time complexity of the Selection Sorting Algorithm is O(n^2), where n is the number of elements in the list. This is due to the nested loops that iterate over the list.











