Last updated on January 13th, 2025 at 09:47 pm

Here, we see a Redundant Connection LeetCode Solution. This Leetcode problem is solved using different approaches in many programming languages, such as C++, Java, JavaScript, Python, etc.

List of all LeetCode Solution

Topics

Array, Dynamic Programming

Companies

Level of Question

Medium

Redundant Connection LeetCode Solution

1. Problem Statement

In this problem, a tree is an undirected graph that is connected and has no cycles.

You are given a graph that started as a tree with n nodes labeled from 1 to n, with one additional edge added. The added edge has two different vertices chosen from 1 to n, and was not an edge that already existed. The graph is represented as an array edges of length n where edges[i] = [a_i, b_i] indicates that there is an edge between nodes a_i and b_i in the graph.

Return an edge that can be removed so that the resulting graph is a tree of n nodes. If there are multiple answers, return the answer that occurs last in the input.

Example 1:

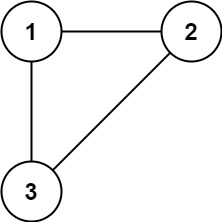
Input: edges = [[1,2],[1,3],[2,3]]
Output: [2,3]

Example 2:

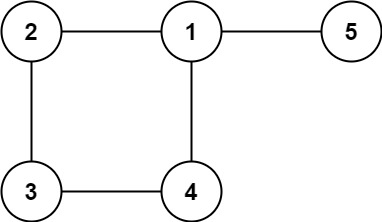
Input: edges = [[1,2],[2,3],[3,4],[1,4],[1,5]]
Output: [1,4]

2. Coding Pattern Used in Solution

The coding pattern used in this code is Union-Find (Disjoint Set Union – DSU). Union-Find is commonly used to solve problems related to connected components in a graph, such as detecting cycles, finding connected components, or determining if two nodes are in the same component.

3. Code Implementation in Different Languages

3.1 Redundant Connection C++

class Solution {
public:
    vector<int> parent;
    vector<int> findRedundantConnection(vector<vector<int>>& edges) {
        if(edges.size()==0) return{};
        parent.resize(edges.size()+1);
        for(int i=1;i<edges.size()+1;i++){
            parent[i]=i;
        }
        for(vector<int> edge : edges){
            int f1=find(edge[0]);
            int f2=find(edge[1]);
            if(f1!=f2)
                parent[f1]=f2;
            else
                return edge;
        }
        return {};
    }
    int find(int x){
        return parent[x]==x ? x : find(parent[x]);
    }
};

3.2 Redundant Connection Java

class Solution {
    public int[] findRedundantConnection(int[][] edges) {
        par = new int[edges.length+1];
        for (int i = 0; i < par.length; i++)
            par[i] = i;
        for (int[] e : edges)
            if (find(e[0]) == find(e[1])) return e;
            else union(e[0],e[1]);
        return edges[0];
    }
    private int[] par;
    private int find(int x) {
        if (x != par[x]) par[x] = find(par[x]);
        return par[x];
    }
    private void union(int x, int y) {
        par[find(y)] = find(x);
    }
}

3.3 Redundant Connection JavaScript

var findRedundantConnection = function(edges) {
    let par = Array.from({length: edges.length + 1}, (_,i) => i)
    const find = x => x === par[x] ? par[x] : par[x] = find(par[x])
    const union = (x,y) => par[find(y)] = find(x)
    for (let [a,b] of edges)
        if (find(a) === find(b)) return [a,b]
        else union(a,b)
};

3.4 Redundant Connection Python

class Solution(object):
    def findRedundantConnection(self, edges):
        par = [i for i in range(len(edges) + 1)]
        def find(x):
            if x != par[x]: par[x] = find(par[x])
            return par[x]
        def union(x, y):
            par[find(y)] = find(x)
        for a,b in edges:
            if find(a) == find(b): return [a,b]
            else: union(a,b)

4. Time and Space Complexity

	Time Complexity	Space Complexity
C++	O(E * α(N))	O(N)
Java	O(E * α(N))	O(N)
JavaScript	O(E * α(N))	O(N)
Python	O(E * α(N))	O(N)

here, E is the number of edges and N is the number of nodes.

The code uses the Union-Find algorithm to detect cycles in a graph.
The time complexity is nearly linear due to the efficient path compression in the find operation.
The space complexity is linear because of the parent array used to store the connected components.