Last updated on September 4th, 2023 at 09:43 pm
Here, We will discuss about Radix Sort in C, their algorithm, implementation code in C, time and space complexity, and their applications.
What is Radix Sort?
Similar to Counting sort and Bucket sort, Radix Sort is a linear sorting algorithm.
The algorithm based on idea that sorting the elements by first grouping the individual digits of the same place value.
For many programs they need a fast sort, Radix sort is a good choice.
Radix sort depends on the digits or letters, so it is less flexible than other sorts.
Radix Sort Algorithm
- Take the least significant digit of each element.
- Sort the list of elements based on that digit, but keep the order of elements with the same digit.
- Repeat the sort with each more significant digit.
The speed of the Radix sort depends on the inner basic operations.
If the operations are not efficient enough, Radix sort can be slower than other algorithms such as Quick Sort and Merge Sort.
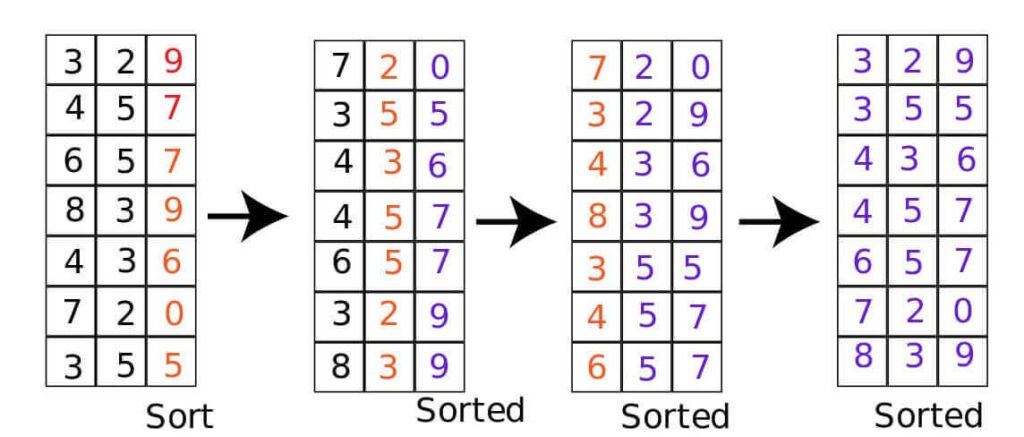
Implementation of Radix Sort
Program code in C
#include<stdio.h>
//function to get the largest element from an array
int getmax(int arr[], int n)
{
int max = arr[0];
for(int i=1; i<n; i++)
if(arr[i] > max)
max = arr[i];
return max;
}
//using counting sort to sort the elements in the basis of significant places
void countingsort(int arr[], int n, int place)
{
int output[n+1];
int max = (arr[0] / place) % 10;
for(int i=1; i<n; i++)
{
if(((arr[i] / place) % 10) > max)
max = arr[i];
}
int count[max+1];
for(int i=0; i<max; i++)
count[i] = 0;
//calculate count of elements
for(int i=0; i<n; i++)
count[(arr[i] / place) % 10]++;
//calculate cummulative count
for(int i=1; i<10; i++)
count[i] += count[i-1];
//place the elements in sorted order
for(int i=n-1; i>=0; i--)
{
output[count[(arr[i] / place)% 10] -1] = arr[i];
count[(arr[i] / place)% 10]--;
}
for(int i=0; i<n; i++)
arr[i] = output[i];
}
//main function to implement radix sort
void radixsort(int arr[], int n)
{
//get maximum element
int max = getmax(arr, n);
//apply counting sort to sort elements based on place value
for(int place=1; max/place>0; place*=10)
countingsort(arr, n, place);
}
//print an array
void printarray(int arr[], int n)
{
for(int i=0; i<n; i++)
{
printf("%d ", arr[i]);
}
printf("\n");
}
//Driver Code
int main()
{
int data[] = {329, 457, 657, 839, 436, 720, 355};
int size = sizeof(data)/sizeof(data[0]);
radixsort(data, size);
printf("Sorted array : ");
printarray(data, size);
}Output
Sorted array : 329 355 436 457 657 720 839Advantages of Radix Sort
- Fast when the keys are short i.e when the range of the array elements is less.
- Used in suffix array construction algorithms like Manber’s algorithm and DC3 algorithm.
Disadvantages of Radix Sort
- Radix Sort depends on digits or letters, so it is less flexible than other sorts.
- The constant for Radix sort is greater compared to other sorting algorithms.
- It takes more space compared to Quick sort which is inplace sorting.
Time and Space Complexity of Radix Sort
| Time Complexity | |
| Worst Case | O(nk) |
| Best Case | O(nk) |
| Average Case | O(nk) |
| Space Complexity | |
| Worst Case | O(n+k) |
Applications of Radix Sort
Radix sort is implemented in
- DC3 algorithm while making a suffix array.
- places where there are numbers in large ranges.
Related:
Want to Contribute:-
If you like “To The Innovation” and want to contribute, you can mail your articles to 📧 contribute@totheinnovation.com. See your articles on the main page and help other coders.😎