Last updated on January 31st, 2025 at 09:32 pm
This article explores the Radix Sort Algorithm, its pseudo code, and how to implement Radix Sort in Python.
Table of Contents
1. What is the Radix Sort Algorithm?
Like Counting and Bucket Sort, the Radix Sort Algorithm is a linear sorting algorithm.
The Radix Sort Algorithm is a non-comparative sorting algorithm that sorts numbers by processing individual digits. It works by sorting numbers based on their least significant digit (LSD) to the most significant digit (MSD) or vice versa. This method is particularly useful for sorting large lists of integers or strings of fixed length.
Radix Sort depends on the digits or letters, so it is less flexible than other sorts.
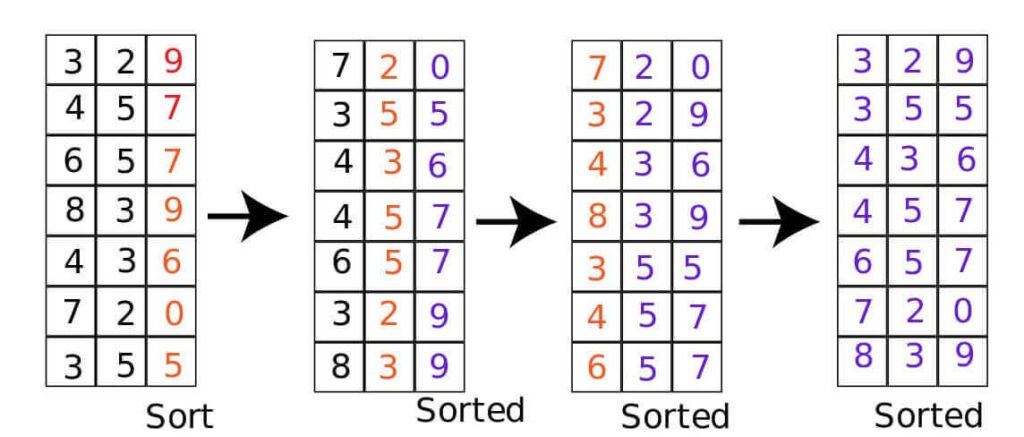
2. How does Radix Sort work?
Step-by-step explanation of how Radix Sort works:
- Identify the Maximum Number of Digits: First, determine the maximum number of digits in the largest number in the dataset. This will dictate the number of passes needed to sort the entire list.
- Sort by Each Digit: Radix Sort processes each digit of the numbers, starting from the least significant digit (rightmost) to the most significant digit (leftmost). Alternatively, it can also work from the most significant to the least significant digit, but the LSD approach is more common.
- Use a Stable Sub-Sorting Algorithm: For each digit position, use a stable sorting algorithm, such as Counting Sort, to sort the numbers. Stability is crucial because it ensures that numbers with the same digit value retain their relative order from previous passes.
- Iterate Through All Digits: Repeat the sorting process for each digit position. After processing all digit positions, the list will be fully sorted.
- Output the Sorted List: Once all digit positions have been processed, the list is sorted, and the algorithm outputs the sorted list.
The Speed of the Radix Sort depends on the inner basic operations. If the operations are not efficient enough, the Radix sort can be slower than other algorithms such as Quick Sort and Merge Sort.
3. Is Radix Sort Stable?
Stability in sorting algorithms means that two equal elements retain their relative order after sorting.
Yes, the Radix Sort Algorithm is stable. Radix Sort maintains stability by using a stable sub-sorting algorithm, such as Counting Sort, at each digit level. This ensures that the order of elements with the same digit value remains unchanged.
4. Pseudo Code for Radix Sort
function radixSort(array)
maxDigitCount = getMaxDigitCount(array)
for digitPosition = 1 to maxDigitCount
countingSortByDigit(array, digitPosition)
end for
end function
function countingSortByDigit(array, digitPosition)
count = array of size 10 initialized to 0
output = array of size of input array
for each number in array
digit = getDigit(number, digitPosition)
count[digit] = count[digit] + 1
end for
for i = 1 to 9
count[i] = count[i] + count[i - 1]
end for
for each number in reverse order of array
digit = getDigit(number, digitPosition)
output[count[digit]] = number
count[digit] = count[digit] - 1
end for
copy output to array
end function
function getDigit(number, digitPosition)
return (number / 10^(digitPosition - 1)) % 10
end function
function getMaxDigitCount(array)
maxNumber = max(array)
return number of digits in maxNumber
end function
5. Radix Sort Python Implementation
Here is a Python implementation of the Radix Sort Algorithm:
def counting_sort(arr, exp):
n = len(arr)
output = [0] * n
count = [0] * 10
for i in range(n):
index = (arr[i] // exp) % 10
count[index] += 1
for i in range(1, 10):
count[i] += count[i - 1]
i = n - 1
while i >= 0:
index = (arr[i] // exp) % 10
output[count[index] - 1] = arr[i]
count[index] -= 1
i -= 1
for i in range(n):
arr[i] = output[i]
def radix_sort(arr):
max_val = max(arr)
exp = 1
while max_val // exp > 0:
counting_sort(arr, exp)
exp *= 10
# Example
arr = [170, 45, 75, 90, 802, 24, 2, 66]
radix_sort(arr)
print("Sorted array is:", arr)
6. Radix Sort Time Complexity and Space Complexity
The time complexity of the Radix Sort Algorithm is O(nk), where n is the number of elements in the array, and k is the number of digits in the largest number. This makes Radix Sort highly efficient for large datasets with a fixed number of digits.
However, its performance can be affected by the choice of the sub-sorting algorithm and the range of input values.
| Time Complexity | |
| Worst Case | O(nk) |
| Best Case | O(nk) |
| Average Case | O(nk) |
| Space Complexity | |
| Worst Case | O(n+k) |
7. Advantages of Radix Sort
- Fast when the keys are short i.e. when the range of the array elements is less.
- Used in suffix array construction algorithms like Manber’s algorithm and DC3 algorithm.
8. Disadvantages of Radix Sort
- Radix Sort depends on digits or letters, so it is less flexible than other sorts.
- The constant for Radix sort is greater compared to other sorting algorithms.
- It takes more space compared to Quick Sort which is in-place sorting.
9. Applications of Radix Sort
Radix sort is implemented in the DC3 algorithm while making a suffix array and places where there are numbers in large ranges.
FAQs
1. Can Radix Sort be used for sorting strings?
Yes, Radix Sort can be adapted to sort strings of fixed length by treating each character as a digit and sorting based on character position.
2. Is Radix Sort suitable for all types of data?
Radix Sort is best suited for sorting integers or strings of fixed length. It may not be the best choice for floating-point numbers or data with varying lengths.
3. How does Radix Sort compare to Quick Sort?
Radix Sort is non-comparative and can be faster than Quick Sort for large datasets with a fixed number of digits. However, Quick Sort is more versatile and can handle a wider range of data types.
4. What is the main advantage of the Radix Sort Algorithm?
The main advantage of the Radix Sort Algorithm is its ability to sort large datasets of integers efficiently without relying on comparisons, making it faster than comparison-based algorithms for specific cases.
5. Is radix sort a stable sorting algorithm?
Yes, Radix Sort is a stable sorting algorithm.
6. Can radix sort be parallelized?
Yes, Radix Sort can be parallelized by distributing the elements into buckets in parallel.
7. What is the time complexity of radix sort?
The time complexity of radix sort is O(nk), where n is the number of elements and k is the number of digits in the radix sort.
8. What is the space complexity of radix sort?
The space complexity of radix sort is O(n + k), where n is the number of elements and k is the number of digits in the radix sort.











