What is the Heap Sort Algorithm and how does it works?

Last updated on January 31st, 2025 at 09:33 pm

This article explores the Heap Sort Algorithm, how it works, pseudocode, implementation in C++, and a comparison with sorted lists in Python.

1. What is the Heap Sort Algorithm?

The Heap Sort Algorithm is a comparison-based sorting algorithm. This sorting algorithm has a more favorable worst-case O(n log n) runtime.

Heap Sort is an in-place algorithm but is not a stable sort meaning it requires a constant amount of additional space.

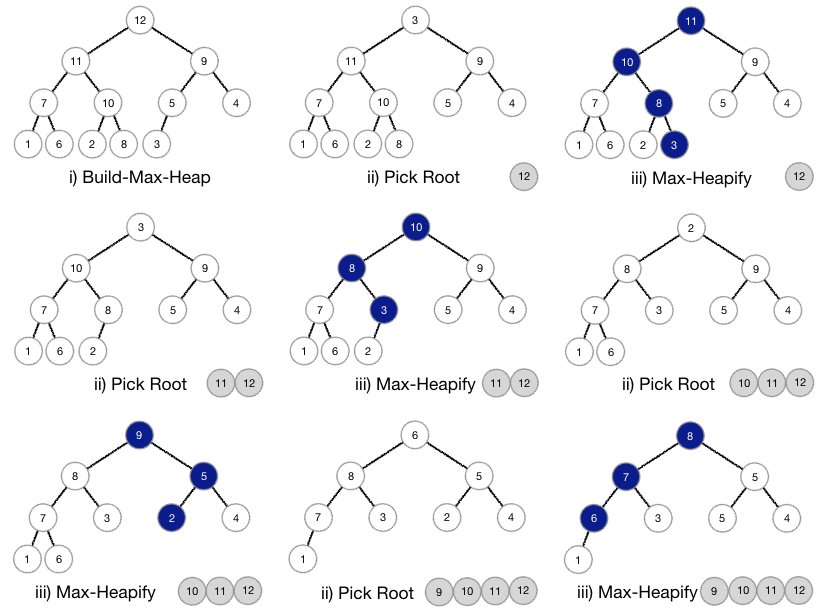
The algorithm works by first building a max heap from the input data, then repeatedly extracting the maximum element from the heap and rebuilding the heap until all elements are sorted.

In max-heaps, the maximum element will always be at the root. Heap Sort uses this property of heap to sort the array.

2. How Does the Heap Sort Algorithm Work?

1. To understand how the Heap Sort Algorithm works, let’s break it down into two main phases:
2. Building the Max Heap:
   • Convert the input array into a max heap, where the largest element is at the root.
   • This is done by calling the heapify function on each non-leaf node, starting from the last non-leaf node up to the root.
3. Extracting Elements from the Heap:
   • Swap the root of the heap with the last element of the heap.
   • Reduce the size of the heap by one and call the heapify function on the root.
   • Repeat the process until the heap size is reduced to one.

3. Is Heap Sort Stable?

A sorting algorithm is considered stable if it maintains the relative order of equal elements. The Heap Sort Algorithm is not stable because the heapify process can change the relative order of equal elements.

However, stability is not always a requirement, and Heap Sort is still a powerful tool for many applications.

4. Heap Sort Pseudocode

Simple pseudocode for the Heap Sort Algorithm:

function heapSort(array):
    n = length(array)
    
    // Build a max heap
    for i = n/2 - 1 down to 0:
        heapify(array, n, i)
    
    // Extract elements from heap
    for i = n - 1 down to 1:
        swap(array[0], array[i])
        heapify(array, i, 0)

function heapify(array, n, i):
    largest = i
    left = 2*i + 1
    right = 2*i + 2
    
    if left < n and array[left] > array[largest]:
        largest = left
    
    if right < n and array[right] > array[largest]:
        largest = right
    
    if largest != i:
        swap(array[i], array[largest])
        heapify(array, n, largest)

5. Implementing the C++ Heap Sort Algorithm

The C++ Heap Sort Algorithm can be implemented using the standard template library (STL) functions like make_heap, push_heap, and pop_heap. These functions simplify the process of building and manipulating heaps, making the implementation more efficient and concise.

#include <iostream>

void heapify(int arr[], int n, int i) {
  int largest = i;
  int left = 2 * i + 1;
  int right = 2 * i + 2;
  if (left < n && arr[left] > arr[largest])
    largest = left;
  if (right < n && arr[right] > arr[largest])
    largest = right;
  if (largest != i) {
    std::swap(arr[i], arr[largest]);
    heapify(arr, n, largest);
  }
}

void heapSort(int arr[], int n) {
  for (int i = n / 2 - 1; i >= 0; i--)
    heapify(arr, n, i);
  for (int i = n - 1; i >= 0; i--) {
    std::swap(arr[0], arr[i]);
    heapify(arr, i, 0);
  }
}

int main() {
  int arr[] = {12, 11, 13, 5, 6, 7};
  int n = sizeof(arr) / sizeof(arr[0]);
  heapSort(arr, n);
  for (int i = 0; i < n; i++)
    std::cout << arr[i] << " ";
  return 0;
}

6. Heap Sort vs Sorted List Python

In Python, the sorted() function uses a sorting algorithm called Timsort, which is a hybrid of Merge Sort and Insertion Sort. While Timsort is generally faster and more efficient than Heap Sort, Heap Sort can still be useful in certain situations, such as when memory is limited or when the input array is very large.

Python implementation of the Heap Sort Algorithm:

def heapify(arr, n, i):
  largest = i
  left = 2 * i + 1
  right = 2 * i + 2
  if left < n and arr[left] > arr[largest]:
    largest = left
  if right < n and arr[right] > arr[largest]:
    largest = right
  if largest != i:
    arr[i], arr[largest] = arr[largest], arr[i]
    heapify(arr, n, largest)

def heapSort(arr):
  n = len(arr)
  for i in range(n // 2 - 1, -1, -1):
    heapify(arr, n, i)
  for i in range(n - 1, 0, -1):
    arr[0], arr[i] = arr[i], arr[0]
    heapify(arr, i, 0)
  return arr

arr = [12, 11, 13, 5, 6, 7]
print(heapSort(arr))

7. Heap Sort Time Complexity and Space Complexity

Time Complexity
Worst Case	O(n log n)
Best Case	O(n log n)
Average Case	O(n log n)
Space Complexity
Worst Case	O(1)

8. Application of Heap Sort

Heap Sort is used when

1. Systems concerned with security and embedded systems such as Linux Kernel.
2. Want to extract the smallest or largest from a list of items without sorting the list.

FAQs