Last updated on January 13th, 2025 at 03:16 am

Here, we see a Delete Node in a BST LeetCode Solution. This Leetcode problem is solved using different approaches in many programming languages, such as C++, Java, JavaScript, Python, etc.

List of all LeetCode Solution

Topics

Tree

Companies

Uber

Level of Question

Medium

Delete Node in a BST LeetCode Solution

1. Problem Statement

Given a root node reference of a BST and a key, delete the node with the given key in the BST. Return the root node reference (possibly updated) of the BST.

Basically, the deletion can be divided into two stages:

Search for a node to remove.
If the node is found, delete the node.

Example 1:

Input: root = [5,3,6,2,4,null,7], key = 3
Output: [5,4,6,2,null,null,7]
Explanation: Given key to delete is 3. So we find the node with value 3 and delete it. One valid answer is [5,4,6,2,null,null,7], shown in the above BST. Please notice that another valid answer is [5,2,6,null,4,null,7] and it’s also accepted.

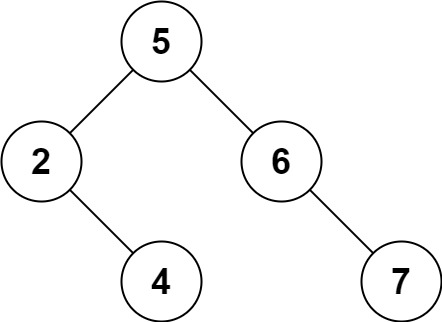
Example 2:
Input: root = [5,3,6,2,4,null,7], key = 0
Output: [5,3,6,2,4,null,7]
Explanation: The tree does not contain a node with value = 0.

Example 3:
Input: root = [], key = 0
Output: []

2. Coding Pattern Used in Solution

The coding pattern used in this code is “Tree Depth First Search (DFS)”. The algorithm traverses the binary search tree (BST) recursively to locate the node to be deleted, and then modifies the tree structure accordingly. The traversal is depth-first because it explores one branch of the tree fully before moving to another branch.

3. Code Implementation in Different Languages

3.1 Delete Node in a BST C++

class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        if(root) 
            if(key < root->val) root->left = deleteNode(root->left, key);
            else if(key > root->val) root->right = deleteNode(root->right, key);       
            else{
                if(!root->left && !root->right) return NULL;
                if (!root->left || !root->right)
                    return root->left ? root->left : root->right; 
                TreeNode* temp = root->left;
                while(temp->right != NULL) temp = temp->right;
                root->val = temp->val;
                root->left = deleteNode(root->left, temp->val);
            }
        return root;
    }   
};

3.2 Delete Node in a BST Java

class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        if(root==null) return null;
        if(key<root.val){                            
            root.left = deleteNode(root.left,key);
            return root;
        }
        else if(key>root.val){
            root.right = deleteNode(root.right,key);
            return root;
        }
        else{
            if(root.left==null){
                return root.right;
            }
            else if(root.right==null){
                return root.left;
            }
            else{
                TreeNode min = root.right;
                while(min.left!=null){
                    min = min.left;
                }
                root.val = min.val;
                root.right = deleteNode(root.right,min.val);
                return root;
            }
        }
    }
}

3.3 Delete Node in a BST JavaScript

var deleteNode = function(root, key) {
    if (null === root) { return null; }
    if (root.val === key) {
        if (null === root.left && null === root.right) { return null; }
        if (null !== root.left && null !== root.right) {
            let curr = root.right;
            while (curr.left) { curr = curr.left; }
            curr.left = root.left;
            return root.right;
        }
        if (null === root.left) { return root.right; }
        if (null === root.right) { return root.left; }
    }
    if (key < root.val) {
        root.left = deleteNode(root.left, key);
    } else {
        root.right = deleteNode(root.right, key);
    }
    return root;
};

3.4 Delete Node in a BST Python

class Solution(object):
    def deleteNode(self, root, key):
        if not root: return None
        if root.val == key:
            if root.left:
                left_right_most = root.left
                while left_right_most.right:
                    left_right_most = left_right_most.right
                left_right_most.right = root.right
                return root.left
            else:
                return root.right
        elif root.val > key:
            root.left = self.deleteNode(root.left, key)
        else:
            root.right = self.deleteNode(root.right, key)
        return root

4. Time and Space Complexity

	Time Complexity (Balanced Tree)	Time Complexity (Skewed Tree)	Space Complexity (Balanced Tree)	Space Complexity (Skewed Tree)
C++	`O(log n)`	`O(n)`	`O(log n)`	`O(n)`
Java	`O(log n)`	`O(n)`	`O(log n)`	`O(n)`
JavaScript	`O(log n)`	`O(n)`	`O(log n)`	`O(n)`
Python	`O(log n)`	`O(n)`	`O(log n)`	`O(n)`

The logic is the same across all four languages, with minor syntactic differences.
The recursive approach ensures that the tree is modified in-place, so no additional data structures are used, keeping the space complexity dependent only on the recursion stack.
The time complexity is determined by the height of the tree, which varies based on whether the tree is balanced or skewed.