Last updated on January 31st, 2025 at 09:15 pm
We’ll discuss types of asymptotic notation, types of notation – theta, big-O, omega, small-o, and small omega notation, the growth rate of an algorithm, analysis of loops – calculation of runtime complexity, and growth of function.
Table of Contents
1. What is Asymptotic Notation?
Asymptotic Notation is used to determine rough estimates of the relative running time of algorithms. It is based on two assumptions, which hold in most of the cases and have their importance. It is very important to understand the assumptions and limitations of asymptotic notations:
- Input Size: how the running time of an algorithm grows for a large input size n
- Constant: The running time of an algorithm also depends on various constants. But for a large input n, the constant factors would be ignored
Example:
| a <- 0 | 1 unit | 1 time |
| for i <- 1 to n do{ | 1 unit | n times |
| for j <- 1 to n do{ | 1 unit | n(n+1)/2 times |
| a <- a+1 | 1 unit | n(n+1)/2 times |
1.1 Theta Notation (Θ-notation)
Theta notation shows the tightest upper bound and the tightest lower bound to the given function. It is used to define the average-case running time.
Big-Theta of g(n), written as f(n) = Θ(g(n))
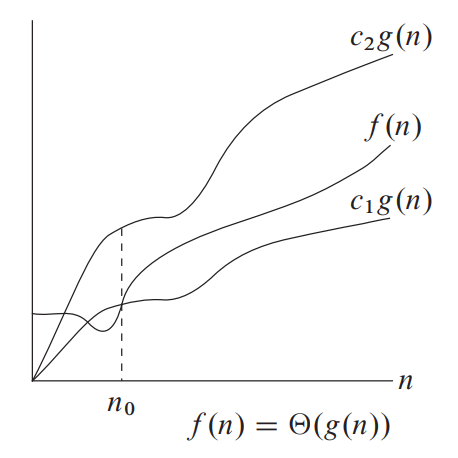
In average case analysis, we take all possible inputs and calculate computing time for all of its inputs.
1.2 Big O Notation (O-notation)
Big-O notation shows the upper bound to the given function. It measures the worst-case time complexity.
Big-O of g(n), written as f(n) = O(g(n))

In the best-case analysis, we calculate lower bound on running time of an algorithm.
1.3 Omega Notation (Ω-notation)
Omega notation shows the lower bound to the given function. It measures the best-case time complexity.
Big-Omega of g(n), written as f(n) = Ω(g(n))

In the best-case analysis, we calculate lower bound on running time of an algorithm
1.4 Small-o Notation (o-notation)
Small-o represents an upper bound which is not a tight upper bound. It is also used to define the worst-case running time
1.5 Small Omega Notation (ω-notation)
Small omega (ω) represents a lower bound which is not a tight lower bound. It is used to define the best-case running time.
Lower Bound <= Average Time <= Upper Bound
2. Types of Complexities
- Constant time complexity: O(1)
- Logarithmic time complexity: O(log(log n)), O(√log )and O(log n)
- Linear time complexity: O(√n) and O(n)
- Polynomial time complexity: O(nk), where k is a constant and is >1
- Exponential time complexity: O(an), where a > 1
3. Asymptotic Growth Rate Notation
Growth Rate of Algorithm is the rate at which the running time increases as a function of input.

log(n!) < (log(n))!
log(log*n) < log*(log n)
n < (log n)log n
2n < n! < nn
3.1 List of the growth rate of an algorithm
| Time Complexity | Name | Example |
|---|---|---|
| O(1) | Constant | Adding an element to the front of a linked list |
| O(log n) | Logarithmic | Finding an element in a sorted array |
| O(n) | Linear | Finding an element in an array |
| O(n log n) | Linear logarithmic | Merging two sorted arrays |
| O(n2) | Quadratic | Shortest path between two nodes in a graph, Bubble sort algorithm |
| O(n3) | Cubic | Matrix Multiplication |
| O(2n) | Exponential | The Tower of Hanoi, Recursive Fibonacci sequence |
4. Analysis Of Loops – Calculate Time Complexity
4.1 O(1) – Constant
The time complexity of a function (or set of statements) is O(1). It doesn’t contain a loop, recursion, or call to any other non-constant time function.
// Here c is a constant
for (int i=1; i<=c; i++)
{
//some O(1) expressions
}4.2 O(n) – Linear
The Time Complexity of a loop is O(n) if the loop variables are incremented/decremented by a constant value.
// Here c is a positive integer constant
for (int i=1; i<=n; i+=c)
{
//some O(1) expressions
}
for (int i=n; i>0; i-=c)
{
//some O(1) expressions
}
4.4 O(nc) – Exponential
The Time Complexity of nested loops is O(nc) if the number of times the innermost statement is executed.
Selection Sort and Insertion Sort have O(n2) time complexity.
for (int i=1; i<=n; i+=c)
{
for (int j=1; j<=n; j+=c)
{
//some O(1) expressions
}
}
for (int i=n; i>0; i+=c)
{
for (int j=i+1; j<=n; j+=c)
{
//some O(1) expressions
}
}4.3 O(log n) – Logarithmic
The Time Complexity of a loop is O(log n) if loop variables are divided/multiplied by a constant value.
main()
{
i=1;
while (i<n)
{
i=2*i;
}
}
5. Growth Rate of Algorithm
The order of growth of the running time of an algorithm gives a simple characterization of the algorithm’s efficiency.
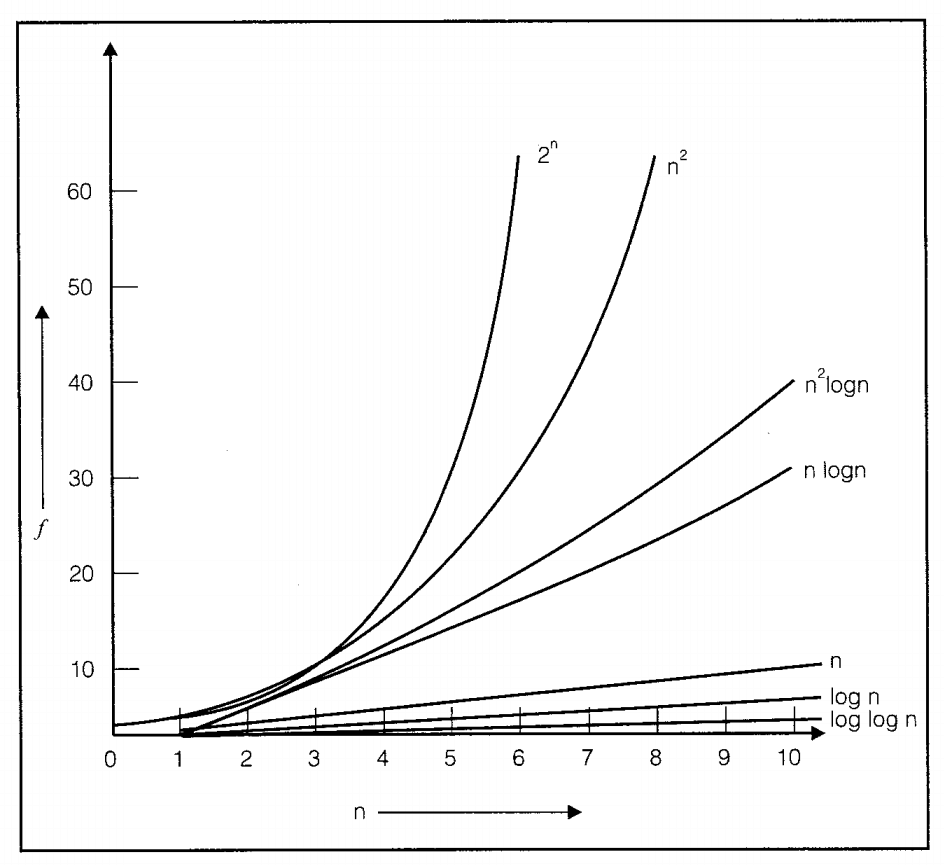
The decreasing order of growth of time complexity is:
22n > n! > 4n > 2n > n2 > n(log n) > log(n!) > n > 2log n > log2 n > √log n > log(log n) >1
FAQs
1. How does Asymptotic Notation help in algorithm design?
Asymptotic Notation provides a standardized way to compare algorithms, aiding in choosing the most efficient one for a given task.
2. Why is asymptotic analysis important?
Asymptotic analysis helps in understanding the efficiency of algorithms, especially for large input sizes. It allows us to compare different algorithms and choose the most efficient one for a given problem.
3. How do I calculate the time complexity of an algorithm?
To calculate the time complexity, you need to analyze the algorithm’s operations and determine how they scale with the input size. This is typically done by counting the number of operations in terms of n (the input size) and expressing it using Big O notation.
4. What is the best-case scenario for an algorithm?
The best-case scenario for an algorithm is described using Big Omega notation. It represents the minimum amount of time or space an algorithm will use for a given input size.











