Last updated on January 31st, 2025 at 09:33 pm
This article explores the Bucket Sort Algorithm, how the Bucket Sort Algorithm works, its pseudocode, time complexity, and implementation in Python.
Table of Contents
1. What is the Bucket Sort Algorithm?
Bucket Sort Algorithm is a comparison sort algorithm. Like Counting sort, Bucket Sort also imposes restrictions on the input to improve the performance.
The Bucket Sort Algorithm is a powerful sorting technique that efficiently organizes elements by distributing them into a number of buckets. Each bucket is then sorted individually, either using a different sorting algorithm or recursively applying the bucket sort. This method is particularly effective for sorting a large number of elements that are uniformly distributed across a range.
Bucket Sort is useful when a large number of elements are uniformly distributed across a range.
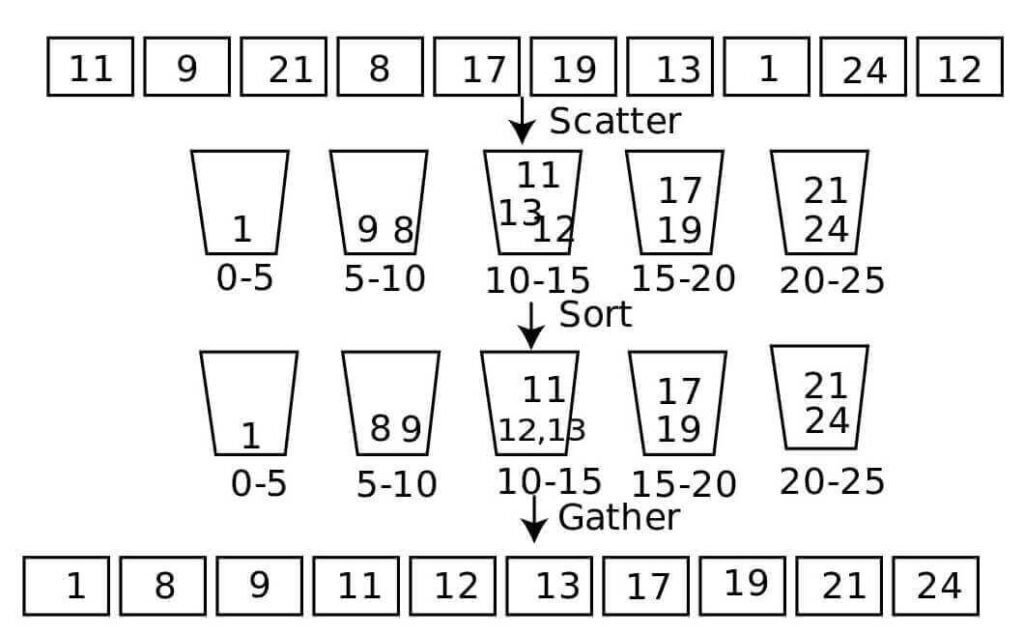
2. How Bucket Sort Works?
The Bucket Sort algorithm works by distributing the elements of an array into a number of buckets. Each bucket is then sorted individually, and the sorted elements are then merged to produce the final sorted array.
Here’s a step-by-step explanation of the Bucket Sort algorithm:
- Create empty buckets.
- Insert elements into their respective buckets.
- Sort each bucket individually.
- Merge the sorted buckets to produce the final sorted array.
3. Bucket Sort Pseudocode
Here’s a simple pseudocode for the Bucket Sort algorithm:
function bucketSort(array, bucketSize) {
if (array.length === 0) {
return array;
}
// Determine minimum and maximum values
let i,
minValue = array[0],
maxValue = array[0];
array.forEach(function (currentVal) {
if (currentVal < minValue) {
minValue = currentVal;
} else if (currentVal > maxValue) {
maxValue = currentVal;
}
});
// Initialize buckets
let bucketCount = Math.floor((maxValue - minValue) / bucketSize) + 1;
let allBuckets = new Array(bucketCount);
for (i = 0; i < allBuckets.length; i++) {
allBuckets[i] = [];
}
// Distribute input array values into buckets
array.forEach(function (currentVal) {
allBuckets[Math.floor((currentVal - minValue) / bucketSize)].push(currentVal);
});
// Sort buckets and place back into input array
array.length = 0;
allBuckets.forEach(function(bucket) {
insertionSort(bucket);
bucket.forEach(function (element) {
array.push(element);
});
});
return array;
}
4. Implementing Bucket Sort in Python
Simple implementation of the Bucket Sort Algorithm in Python:
def bucket_sort(arr):
if len(arr) == 0:
return arr
# Create buckets
bucket_count = len(arr)
max_value = max(arr)
min_value = min(arr)
bucket_range = (max_value - min_value) / bucket_count
buckets = [[] for _ in range(bucket_count)]
# Distribute input array values into buckets
for i in range(len(arr)):
diff = (arr[i] - min_value) / bucket_range - int((arr[i] - min_value) / bucket_range)
if diff == 0 and arr[i] != min_value:
buckets[int((arr[i] - min_value) / bucket_range) - 1].append(arr[i])
else:
buckets[int((arr[i] - min_value) / bucket_range)].append(arr[i])
# Sort each bucket and concatenate
sorted_array = []
for bucket in buckets:
sorted_array.extend(sorted(bucket))
return sorted_array
# Example
arr = [0.42, 0.32, 0.23, 0.52, 0.25, 0.47, 0.51]
print(bucket_sort(arr))
5. When to Use Bucket Sort?
The Bucket Sort Algorithm is most effective when:
- The input is uniformly distributed.
- The range of input values is known and not too large.
- The number of buckets is chosen appropriately.
Bucket Sort may not be the best choice for sorting arrays with a large number of duplicate elements or arrays with a large range of values.
6. Bucket Sort Time Complexity and Space Complexity
| Time Complexity | |
| Worst Case | O(n2) |
| Best Case | O(n+k) |
| Average Case | O(n+k) |
| Space Complexity | |
| Worst Case | O(n) |
7. Advantages and Disadvantages of Bucket Sort
7.1 Advantages
- Bucket Sort has a linear time complexity in the best-case scenario.
- It’s suitable for sorting arrays with a limited range of values.
- It’s relatively simple to implement.
7.2 Disadvantages
- Bucket Sort has a quadratic time complexity in the worst-case scenario.
- It’s not suitable for sorting arrays with a large range of values.
- It’s not a stable sorting algorithm.
FAQs
1. What is the Bucket Sort Algorithm?
The Bucket Sort Algorithm is a sorting technique that distributes elements into buckets and sorts each bucket individually.
2. How does Bucket Sort work?
Bucket Sort works by dividing the input into several buckets, sorting each bucket, and then concatenating the sorted buckets.
3. When should I use Bucket Sort?
Use Bucket Sort when the input data is uniformly distributed and the range of values is known.
4. Can Bucket Sort be used for integers?
Yes, Bucket Sort can be adapted for integers, especially when they are within a specific range.
5. Is Bucket Sort a stable sorting algorithm?
No, Bucket Sort is not a stable sorting algorithm.
6. Can Bucket Sort be used for sorting arrays with duplicate elements?
Yes, Bucket Sort can be used for sorting arrays with duplicate elements. However, it may not be the best choice for arrays with a large number of duplicate elements.
7. When should I avoid using Bucket Sort?
Avoid Bucket Sort when the input data is already partially sorted or has a non-uniform distribution. In such cases, other sorting algorithms might provide better time complexity.
8. What is the time complexity of Bucket Sort?
The average time complexity of Bucket Sort is O(n + k), but it can degrade to O(n^2) in the worst case.











