Last updated on February 2nd, 2025 at 06:14 am
Here, we see a Trim a Binary Search Tree LeetCode Solution. This Leetcode problem is solved using different approaches in many programming languages, such as C++, Java, JavaScript, Python, etc.
List of all LeetCode Solution
Topics
Tree
Companies
Bloomberg
Level of Question
Medium

Trim a Binary Search Tree LeetCode Solution
Table of Contents
1. Problem Statement
Given the root of a binary search tree and the lowest and highest boundaries as low and high, trim the tree so that all its elements lies in [low, high]. Trimming the tree should not change the relative structure of the elements that will remain in the tree (i.e., any node’s descendant should remain a descendant). It can be proven that there is a unique answer.
Return the root of the trimmed binary search tree. Note that the root may change depending on the given bounds.
Example 1:
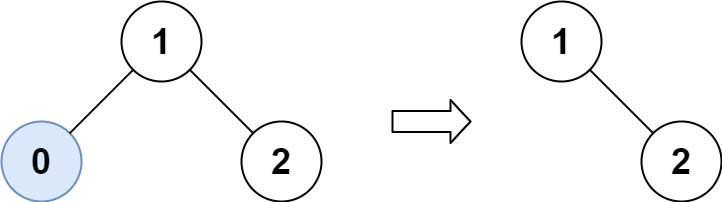
Input: root = [1,0,2], low = 1, high = 2
Output: [1,null,2]
Example 2:
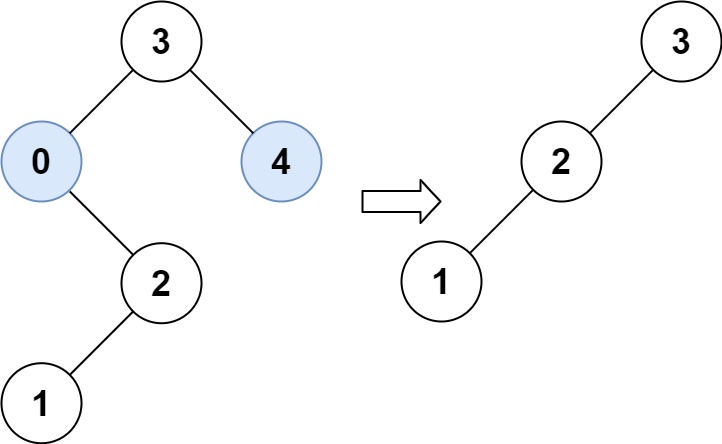
Input: root = [3,0,4,null,2,null,null,1], low = 1, high = 3
Output: [3,2,null,1]
2. Coding Pattern Used in Solution
The coding pattern used in this code is Tree Depth First Search (DFS). The algorithm traverses the binary search tree (BST) recursively in a depth-first manner to trim nodes that fall outside the range [low, high]. The traversal ensures that the tree structure is preserved while removing nodes that do not satisfy the condition.
3. Code Implementation in Different Languages
3.1 Trim a Binary Search Tree C++
class Solution {
public:
TreeNode* trimBST(TreeNode* root, int low, int high) {
if (!root) {
return root;
}
if (root->val >= low && root->val <= high) {
root->left = trimBST(root->left, low, high);
root->right = trimBST(root->right, low, high);
return root;
}
if (root->val < low) {
return trimBST(root->right, low, high);
}
return trimBST(root->left, low, high);
}
};
3.2 Trim a Binary Search Tree Java
class Solution {
public TreeNode trimBST(TreeNode root, int low, int high) {
if (root == null) {
return null;
}
if (root.val >= low && root.val <= high) {
root.left = trimBST(root.left, low, high);
root.right = trimBST(root.right, low, high);
} else if (root.val < low) {
root = trimBST(root.right, low, high);
} else if (root.val > high) {
root = trimBST(root.left, low, high);
}
return root;
}
}
3.3 Trim a Binary Search Tree JavaScript
var trimBST = function(root, low, high) {
if (root === null) {
return null;
}
if (root.val > high) {
return trimBST(root.left, low,high);
}
if (root.val < low) {
return trimBST(root.right, low, high);
}
root.left = trimBST(root.left, low, high);
root.right = trimBST(root.right, low, high);
return root;
};
3.4 Trim a Binary Search Tree Python
class Solution(object):
def trimBST(self, root, low, high):
if not root: return root
if root.val < low: return self.trimBST(root.right, low, high)
if root.val > high: return self.trimBST(root.left, low, high)
root.left = self.trimBST(root.left, low, high)
root.right = self.trimBST(root.right, low, high)
return root
4. Time and Space Complexity
| Time Complexity | Space Complexity | |
| C++ | O(N) | O(H) |
| Java | O(N) | O(H) |
| JavaScript | O(N) | O(H) |
| Python | O(N) | O(H) |
where, N is the number of nodes in the tree and H is the height of the tree.
- The code leverages the properties of a binary search tree (BST) to efficiently decide whether to keep or discard subtrees.
- The recursive approach ensures that the tree structure is preserved while trimming nodes outside the range
[low, high]. - The algorithm is optimal for this problem as it avoids unnecessary traversal of subtrees that are guaranteed to be out of range.