Last updated on March 2nd, 2025 at 03:50 pm
Here, we see a Transform to Chessboard LeetCode Solution. This Leetcode problem is solved using different approaches in many programming languages, such as C++, Java, JavaScript, Python, etc.
List of all LeetCode Solution
Topics
Hash Table
Level of Question
Hard

Transform to Chessboard LeetCode Solution
Table of Contents
1. Problem Statement
You are given an n x n binary grid board. In each move, you can swap any two rows with each other, or any two columns with each other.
Return the minimum number of moves to transform the board into a chessboard board. If the task is impossible, return -1.
A chessboard board is a board where no 0‘s and no 1‘s are 4-directionally adjacent.
Example 1:
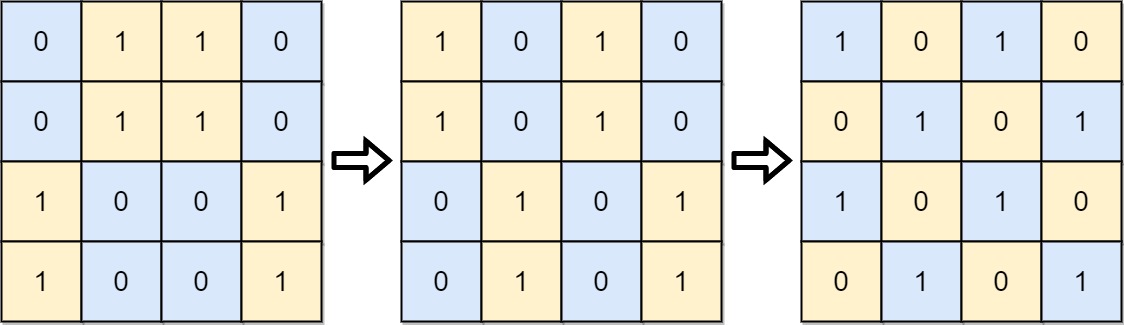
Input: board = [[0,1,1,0],[0,1,1,0],[1,0,0,1],[1,0,0,1]] Output: 2 Explanation: One potential sequence of moves is shown. The first move swaps the first and second column. The second move swaps the second and third row.
Example 2:
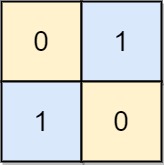
Input: board = [[0,1],[1,0]] Output: 0 Explanation: Also note that the board with 0 in the top left corner, is also a valid chessboard.
Example 3:
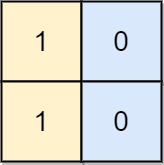
Input: board = [[1,0],[1,0]] Output: -1 Explanation: No matter what sequence of moves you make, you cannot end with a valid chessboard.
2. Coding Pattern Used in Solution
The coding pattern used in this problem is Matrix Transformation. This pattern involves analyzing and transforming a 2D matrix to meet specific conditions. The problem requires checking if a given board can be transformed into a valid chessboard and calculating the minimum number of swaps required to achieve this transformation.
It is a specialized problem-solving approach for matrix-based problems.
3. Code Implementation in Different Languages
3.1 Transform to Chessboard C++
class Solution {
public:
int movesToChessboard(vector<vector<int>>& board) {
int n = board.size();
int row_counter = 0, col_counter = 0;
for(int r = 0; r < n; r++){
row_counter += board[r][0] ? 1 : -1;
for(int c = 0; c < n; c++){
if(r == 0) col_counter += board[r][c] ? 1 : -1;
if((board[r][0] ^ board[0][0]) ^ (board[r][c] ^ board[0][c])) return -1;
}
}
if(abs(row_counter) > 1 || abs(col_counter) > 1) return -1;
int row_swap_count = 0, col_swap_count = 0, row_0_count = 0, col_0_count = 0;
for(int i = 0; i < n; i++){
if(i & 1){
row_swap_count += board[i][0];
col_swap_count += board[0][i];
}
row_0_count += board[i][0] == 0, col_0_count += board[0][i] == 0;
}
int odd_position_count = n/2;
if(n & 1){
row_swap_count = row_0_count == odd_position_count ? row_swap_count : (odd_position_count - row_swap_count);
col_swap_count = col_0_count == odd_position_count ? col_swap_count : (odd_position_count - col_swap_count);
}
else{
row_swap_count = min(row_swap_count, odd_position_count - row_swap_count);
col_swap_count = min(col_swap_count, odd_position_count - col_swap_count);
}
return row_swap_count + col_swap_count;
}
};
3.2 Transform to Chessboard Java
class Solution {
public int movesToChessboard(int[][] board) {
int N = board.length, rowSum = 0, colSum = 0, rowSwap = 0, colSwap = 0;
for (int r = 0; r < N; ++r)
for (int c = 0; c < N; ++c) {
if ((board[0][0] ^ board[r][0] ^ board[0][c] ^ board[r][c]) == 1)
return -1;
}
for (int i = 0; i < N; ++i) {
rowSum += board[0][i];
colSum += board[i][0];
rowSwap += board[i][0] == i % 2 ? 1 : 0;
colSwap += board[0][i] == i % 2 ? 1 : 0;
}
if (N / 2 > rowSum || rowSum > (N + 1) / 2) return -1;
if (N / 2 > colSum || colSum > (N + 1) / 2) return -1;
if (N % 2 == 1) {
if (colSwap % 2 == 1) colSwap = N - colSwap;
if (rowSwap % 2 == 1) rowSwap = N - rowSwap;
} else {
colSwap = Math.min(N - colSwap, colSwap);
rowSwap = Math.min(N - rowSwap, rowSwap);
}
return (colSwap + rowSwap) / 2;
}
}
3.3 Transform to Chessboard JavaScript
var movesToChessboard = function (board) {
let boardSize = board.length;
let boardSizeIsEven = boardSize % 2 === 0;
if (!canBeTransformed(board)) return -1;
let rowSwap = 0;
let colSwap = 0;
let rowSwap2 = 0;
let colSwap2 = 0;
for (let i = 0; i < boardSize; i++) {
if (board[i][0] === i % 2) {
rowSwap++;
} else {
rowSwap2++;
}
if (board[0][i] === i % 2) {
colSwap++;
} else {
colSwap2++;
}
}
if ((rowSwap + colSwap) === 0 || (rowSwap2 + colSwap2) === 0) return 0;
if (boardSizeIsEven) {
rowSwap = Math.min(rowSwap, rowSwap2);
colSwap = Math.min(colSwap, colSwap2);
} else {
rowSwap = rowSwap % 2 === 0 ? rowSwap : rowSwap2;
colSwap = colSwap % 2 === 0 ? colSwap : colSwap2;
}
return (rowSwap + colSwap) / 2;
function canBeTransformed(board) {
let sum = board[0].reduce((a, b) => a + b);
if (boardSizeIsEven && sum != boardSize / 2) return false;
if (!boardSizeIsEven && sum > ((boardSize + 1) / 2)) return false;
let first = board[0].join('');
let opposite = board[0].map((item) => item === 1 ? 0 : 1).join('');
let counter = [0, 0];
for (let i = 0; i < boardSize; i++) {
let str = board[i].join('');
if (str == first) {
counter[0]++;
} else if (str == opposite) {
counter[1]++;
} else {
return false;
}
}
if (boardSizeIsEven) {
return counter[0] == counter[1];
}
return Math.abs(counter[0] - counter[1]) === 1
}
};
3.4 Transform to Chessboard Python
class Solution(object):
def movesToChessboard(self, board):
self.set_up_for_processing_board(len(board))
return self.process_board(board)
def check_even(self, count) :
if len(count) != 2 or sorted(count.values()) != self.balanced :
return -1
return 1
def all_opposite(self, line1, line2) :
if not all (line1_value ^ line2_value for line1_value, line2_value in zip(line1, line2)) :
return -1
return 1
def set_sums_of_lists_of_values(self) :
self.sums_of_lists_of_values = [sum(list_of_values) for list_of_values in self.lists_of_values]
def update_number_of_swaps(self) :
self.number_of_swaps += min(self.sums_of_lists_of_values) // 2
def set_lists_of_values(self, line1) :
self.lists_of_values = []
for start in self.starts :
new_list = []
for index, value in enumerate(line1, start) :
new_list.append((index-value) % 2)
self.lists_of_values.append(new_list)
def set_starting_values(self, line1) :
self.starts = [+(line1.count(1) * 2 > self.n)] if self.n & 1 else [0, 1]
def process_line(self, line1) :
self.set_starting_values(line1)
self.set_lists_of_values(line1)
self.set_sums_of_lists_of_values()
self.update_number_of_swaps()
def process_board(self, board) :
for count in (collections.Counter(map(tuple, board)), collections.Counter(zip(*board))) :
if self.check_even(count) == -1 :
return -1
line1, line2 = count
if self.all_opposite(line1, line2) == -1 :
return -1
self.process_line(line1)
return self.number_of_swaps
def set_up_for_processing_board(self, n) :
self.n = n
self.number_of_swaps = 0
self.balanced = [n//2, (n+1)//2]
4. Time and Space Complexity
| Time Complexity | Space Complexity | |
| C++ | O(n²) | O(1) |
| Java | O(n²) | O(1) |
| JavaScript | O(n²) | O(1) |
| Python | O(n²) | O(n) |
- The problem is a Matrix Transformation problem, requiring validation and transformation of a 2D matrix.
- The code uses bitwise XOR operations to validate the board and determine the number of swaps.
- The time complexity is O(N²) due to the nested loops over the board, and the space complexity varies slightly depending on the language.