Last updated on March 1st, 2025 at 09:11 pm
Here, we see The Skyline Problem LeetCode Solution. This Leetcode problem is solved using different approaches in many programming languages, such as C++, Java, JavaScript, Python, etc.
List of all LeetCode Solution
Topics
Binary Indexed Tree, Divide and Conquer, Heap, Line-sweep, Segment-Tree
Companies
Facebook, Google, Microsoft, Twitter, Yelp
Level of Question
Hard

The Skyline Problem LeetCode Solution
Table of Contents
1. Problem Statement
A city’s skyline is the outer contour of the silhouette formed by all the buildings in that city when viewed from a distance. Given the locations and heights of all the buildings, return the skyline formed by these buildings collectively.
The geometric information of each building is given in the array buildings where buildings[i] = [lefti, righti, heighti]:
leftiis the x coordinate of the left edge of theithbuilding.rightiis the x coordinate of the right edge of theithbuilding.heightiis the height of theithbuilding.
You may assume all buildings are perfect rectangles grounded on an absolutely flat surface at height 0.
The skyline should be represented as a list of “key points” sorted by their x-coordinate in the form [[x1,y1],[x2,y2],...]. Each key point is the left endpoint of some horizontal segment in the skyline except the last point in the list, which always has a y-coordinate 0 and is used to mark the skyline’s termination where the rightmost building ends. Any ground between the leftmost and rightmost buildings should be part of the skyline’s contour.
Note: There must be no consecutive horizontal lines of equal height in the output skyline. For instance, [...,[2 3],[4 5],[7 5],[11 5],[12 7],...] is not acceptable; the three lines of height 5 should be merged into one in the final output as such: [...,[2 3],[4 5],[12 7],...]
Example 1:
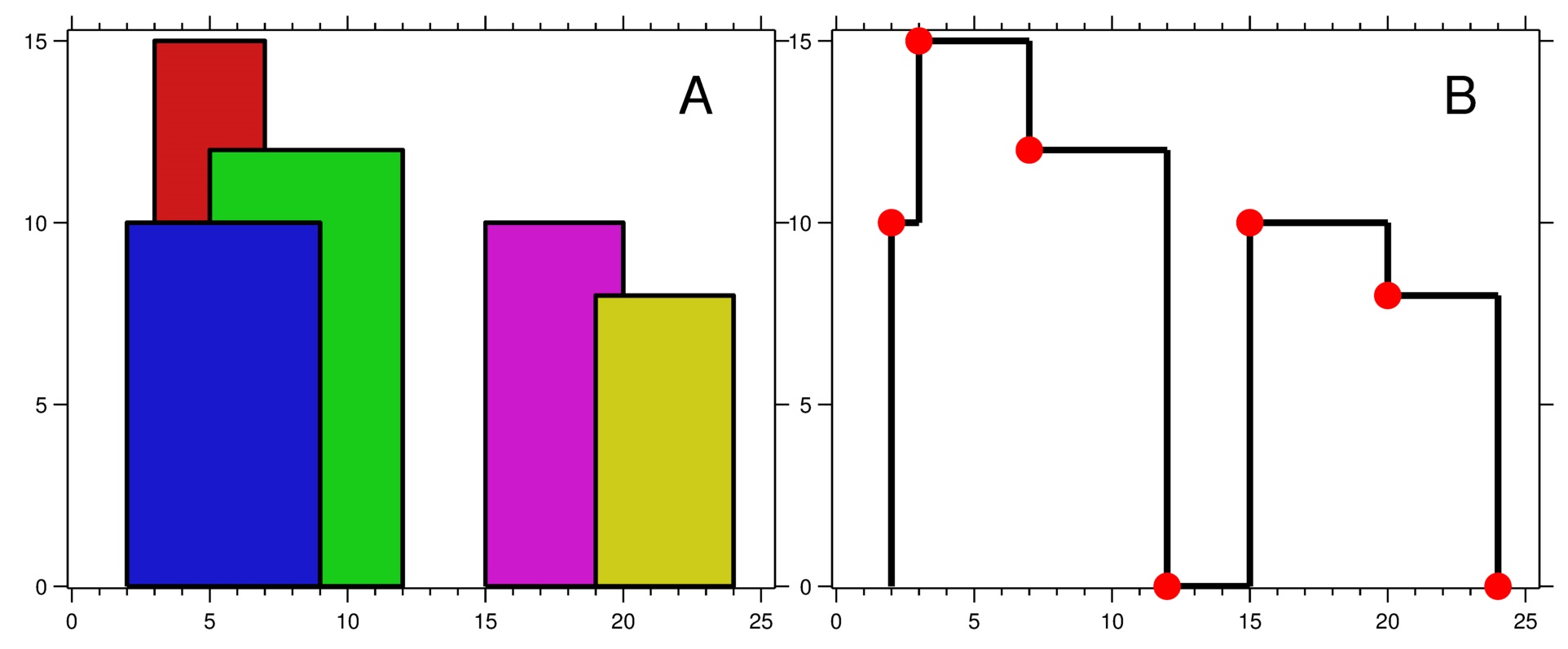
Input: buildings = [[2,9,10],[3,7,15],[5,12,12],[15,20,10],[19,24,8]]
Output: [[2,10],[3,15],[7,12],[12,0],[15,10],[20,8],[24,0]]
Explanation: Figure A shows the buildings of the input. Figure B shows the skyline formed by those buildings. The red points in figure B represent the key points in the output list.
Example 2:
Input: buildings = [[0,2,3],[2,5,3]]
Output: [[0,3],[5,0]]
2. Coding Pattern Used in Solution
The coding pattern used in all the implementations is “Sweep Line Algorithm with Priority Queue”. The algorithm processes events (building start and end points) in sorted order and uses a priority queue (or similar data structure) to maintain the current active heights of buildings. This allows efficient determination of the skyline.
3. Code Implementation in Different Languages
3.1 The Skyline Problem C++
class Solution {
public:
vector<vector<int>> getSkyline(vector<vector<int>>& buildings) {
int edge_idx = 0;
vector<pair<int, int>> edges;
priority_queue<pair<int, int>> pq;
vector<vector<int>> skyline;
for (int i = 0; i < buildings.size(); ++i) {
const auto &b = buildings[i];
edges.emplace_back(b[0], i);
edges.emplace_back(b[1], i);
}
std::sort(edges.begin(), edges.end());
while (edge_idx < edges.size()) {
int curr_height;
const auto &[curr_x, _] = edges[edge_idx];
while (edge_idx < edges.size() &&
curr_x == edges[edge_idx].first) {
const auto &[_, building_idx] = edges[edge_idx];
const auto &b = buildings[building_idx];
if (b[0] == curr_x)
pq.emplace(b[2], b[1]);
++edge_idx;
}
while (!pq.empty() && pq.top().second <= curr_x)
pq.pop();
curr_height = pq.empty() ? 0 : pq.top().first;
if (skyline.empty() || skyline.back()[1] != curr_height)
skyline.push_back({curr_x, curr_height});
}
return skyline;
}
};
3.2 The Skyline Problem Java
class TopNode {
int x;
int h;
TopNode next;
TopNode() {
}
TopNode(int x, int h) {
this.x = x;
this.h = h;
}
void insert(TopNode n) {
n.next = next;
next = n;
}
}
class Solution {
static final int LEFT=0, RIGHT=1, HEIGHT=2;
public List<List<Integer>> getSkyline(int[][] buildings) {
TopNode head = new TopNode(0,0);
head.insert(new TopNode(Integer.MAX_VALUE, 0));
TopNode start = head;
for (int i = 0; i<buildings.length; i++) {
int[] b = buildings[i];
int bL = buildings[i][LEFT];
int bR = buildings[i][RIGHT];
int bH = buildings[i][HEIGHT];
//System.out.println(Arrays.toString(buildings[i]));
while (bL >= start.next.x) { start = start.next; }
//System.out.println(start.toString());
for (TopNode t = start ; bR > t.x; t = t.next) {
//System.out.println(head.toString());
if (bH <= t.h) {
continue;
}
TopNode stop = t;
while (stop.next != null && stop.next.x < bR && stop.next.h <= bH ) {
stop = stop.next;
}
if (bL <= t.x) {
if (bR >= stop.next.x) {
t.next = stop.next;
t.h = bH;
}
else if (t == stop) {
t.insert(new TopNode(bR,t.h));
t.h = bH;
break;
}
else {
stop.x = bR;
t.h = bH;
t.next = stop;
break;
}
}
else {
if (bR >= stop.next.x) {
if (t == stop) {
t.insert(new TopNode(bL, bH));
}
else {
t.next = stop;
stop.x = bL;
stop.h = bH;
}
break;
}
else if (t == stop) {
t.insert(new TopNode(bL,bH));
t.next.insert(new TopNode(bR,t.h));
break;
}
else {
t.next = stop;
t.insert(new TopNode(bL,bH));
stop.x = bR;
break;
}
}
t = stop;
}
}
List<List<Integer>> skyline = new ArrayList<>();
if (head.h == 0)
head = head.next;
while (head != null) {
int height = head.h;
skyline.add(List.of(head.x, height));
while ( (head = head.next) != null && head.h == height) {}
}
return skyline;
}
}
3.3 The Skyline Problem JavaScript
var getSkyline = function(buildings) {
const data = [];
for (let [x1, x2, h] of buildings) {
data.push([x1, h], [x2, -h]);
}
data.sort(([x1, h1], [x2, h2]) => x1 - x2 || h2 - h1);
const heights = [];
const addHeight = (heights, h) => {
let left = 0;
let right = heights.length - 1;
while (left <= right) {
const mid = Math.floor((left + right) / 2);
if (heights[mid] >= h) {
right = mid - 1;
} else {
left = mid + 1;
}
}
heights.splice(left, 0, h);
}
const removeHeight = (heights, h) => {
let left = 0;
let right = heights.length - 1;
while (left <= right) {
const mid = Math.floor((left + right) / 2);
if (heights[mid] >= h) {
right = mid - 1;
} else {
left = mid + 1;
}
}
heights.splice(left, 1);
}
const answer = [];
let previousHeight = 0;
for (let [x, h] of data) {
if (h > 0) {
addHeight(heights, h);
} else {
removeHeight(heights, -h);
}
let currentHeight = heights[heights.length - 1] || 0;
if (currentHeight !== previousHeight) {
answer.push([x, currentHeight]);
previousHeight = currentHeight;
}
}
return answer;
};
3.4 The Skyline Problem Python
class Solution(object):
def getSkyline(self, buildings):
x_height_right_tuples = sorted([(L, -H, R) for L, R, H in buildings] + [(R, 0, "doesn't matter") for _, R, _ in buildings])
result, max_heap = [[0, 0]], [(0, float('inf'))]
for x, negative_height, R in x_height_right_tuples:
while x >= max_heap[0][1]:
heapq.heappop(max_heap)
if negative_height:
heapq.heappush(max_heap, (negative_height, R))
curr_max_height = -max_heap[0][0]
if result[-1][1] != curr_max_height:
result.append([x, curr_max_height])
return result[1:]
4. Time and Space Complexity
| Time Complexity | Space Complexity | |
| C++ | O(n log n) | O(n) |
| Java | O(n2) | O(n) |
| JavaScript | O(n log n) | O(n) |
| Python | O(n log n) | O(n) |
where n is the number of buildings.