Last updated on January 19th, 2025 at 02:37 am

Here, we see a Swim in Rising Water LeetCode Solution. This Leetcode problem is solved using different approaches in many programming languages, such as C++, Java, JavaScript, Python, etc.

List of all LeetCode Solution

Topics

Greedy, Heap, Sort, String

Level of Question

Hard

Swim in Rising Water LeetCode Solution

1. Problem Statement

You are given an n x n integer matrix grid where each value grid[i][j] represents the elevation at that point (i, j).

The rain starts to fall. At time t, the depth of the water everywhere is t. You can swim from a square to another 4-directionally adjacent square if and only if the elevation of both squares individually are at most t. You can swim infinite distances in zero time. Of course, you must stay within the boundaries of the grid during your swim.

Return the least time until you can reach the bottom right square (n - 1, n - 1) if you start at the top left square (0, 0).

Example 1:

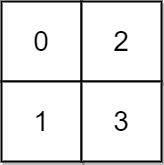
Input: grid = [[0,2],[1,3]] Output: 3 Explanation: At time 0, you are in grid location (0, 0). You cannot go anywhere else because 4-directionally adjacent neighbors have a higher elevation than t = 0. You cannot reach point (1, 1) until time 3. When the depth of water is 3, we can swim anywhere inside the grid.

Example 2:

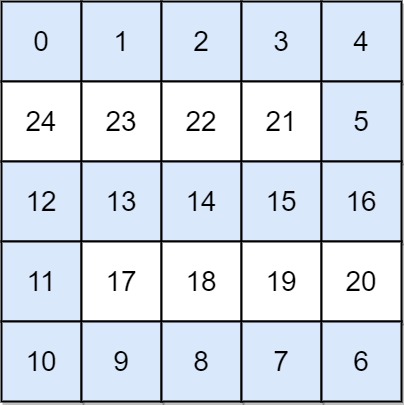
Input: grid = [[0,1,2,3,4],[24,23,22,21,5],[12,13,14,15,16],[11,17,18,19,20],[10,9,8,7,6]] Output: 16 Explanation: The final route is shown. We need to wait until time 16 so that (0, 0) and (4, 4) are connected.

2. Coding Pattern Used in Solution

The coding pattern used in this problem is “Graph Traversal with Priority Queue (Dijkstra-like Algorithm)”. The algorithm uses a priority queue (min-heap) to explore the grid in increasing order of elevation, ensuring that the path with the minimum “maximum elevation” is found.

3. Code Implementation in Different Languages

3.1 Swim in Rising Water C++

class Solution {
public:
    int swimInWater(vector<vector<int>>& grid) {
        int n = grid.size();
        if (n == 1) {
            return 0;
        }
        vector<vector<bool>> visited(n, vector<bool>(n));
        visited[0][0] = true;
        int result = max(grid[0][0], grid[n - 1][n - 1]);
        priority_queue<vector<int>, vector<vector<int>>, greater<vector<int>>> pq;
        pq.push({result, 0, 0});
        while (!pq.empty()) {
            vector<int> curr = pq.top();
            pq.pop();
            result = max(result, curr[0]);
            for (int i = 0; i < 4; i++) {
                int x = curr[1] + dirs[i][0];
                int y = curr[2] + dirs[i][1];
                if (x < 0 || x >= n || y < 0 || y >= n || visited[x][y]) {
                    continue;
                }
                if (x == n - 1 && y == n - 1) {
                    return result;
                }
                pq.push({grid[x][y], x, y});
                visited[x][y] = true;
            }
        }
        return -1;
    }
private:
    vector<vector<int>> dirs = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
};

3.2 Swim in Rising Water Java

class Solution {
    public int swimInWater(int[][] grid) {
        PriorityQueue<Integer> pq = new PriorityQueue<>();
        int N = grid.length - 1, ans = grid[0][0], i = 0, j = 0;
        while (i < N || j < N) {
            for (int[] m : moves) {
                int ia = i + m[0], jb = j + m[1];
                if (ia < 0 || ia > N || jb < 0 || jb > N || grid[ia][jb] > 2500) continue;
                pq.add((grid[ia][jb] << 12) + (ia << 6) + jb);
                grid[ia][jb] = 3000;
            }
            int next = pq.poll();
            ans = Math.max(ans, next >> 12);
            i = (next >> 6) & ((1 << 6) - 1);
            j = next & ((1 << 6) - 1);
        }
        return ans;
    }
    private int[][] moves = {{1,0},{0,1},{-1,0},{0,-1}};
}

3.3 Swim in Rising Water JavaScript

const moves = [[1,0],[0,1],[-1,0],[0,-1]]

var swimInWater = function(grid) {
    let pq = new MinPriorityQueue(),
        N = grid.length - 1, ans = grid[0][0], i = 0, j = 0
    while (i < N || j < N) {
        for (let [a,b] of moves) {
            let ia = i + a, jb = j + b
            if (ia < 0 || ia > N || jb < 0 || jb > N || grid[ia][jb] > 2500) continue
            pq.enqueue((grid[ia][jb] << 12) + (ia << 6) + jb)
            grid[ia][jb] = 3000
        }
        let next = pq.dequeue().element
        ans = Math.max(ans, next >> 12)
        i = (next >> 6) & ((1 << 6) - 1)
        j = next & ((1 << 6) - 1)
    }
    return ans
};

3.4 Swim in Rising Water Python

class Solution(object):
    def swimInWater(self, grid):
        N = len(grid)
        visit = set()
        minH = [[grid[0][0], 0, 0]]
        directions = [[0, 1], [0, -1], [1, 0], [-1, 0]]
        visit.add((0, 0))
        while minH:
            t, r, c = heapq.heappop(minH)
            if r == N - 1 and c == N - 1:
                return t
            for dr, dc in directions:
                neiR, neiC = r + dr, c + dc
                if (neiR < 0 or neiC < 0 or neiR == N or neiC == N or (neiR, neiC) in visit):
                    continue
                visit.add((neiR, neiC))
                heapq.heappush(minH, [max(t, grid[neiR][neiC]), neiR, neiC])

4. Time and Space Complexity

	Time Complexity	Space Complexity
C++	O(n² \ log n)	O(n²)
Java	O(n² \ log n)	O(n²)
JavaScript	O(n² \ log n)	O(n²)
Python	O(n² \ log n)	O(n²)

The algorithm is essentially a Dijkstra-like shortest path algorithm applied to a grid, where the “weight” of a cell is its elevation.
The priority queue ensures that the algorithm always processes the cell with the smallest elevation first, which is critical for finding the minimum “maximum elevation” path.
The space complexity is dominated by the size of the priority queue and the visited set/array, both of which grow proportionally to the number of cells in the grid (n²).