Last updated on February 9th, 2025 at 04:31 am
Here, we see a Search a 2D Matrix II LeetCode Solution. This Leetcode problem is solved using different approaches in many programming languages, such as C++, Java, JavaScript, Python, etc.
List of all LeetCode Solution
Topics
Companies
Amazon, Apple, Google
Level of Question
Medium

Search a 2D Matrix II LeetCode Solution
Table of Contents
1. Problem Statement
Write an efficient algorithm that searches for a value target in an m x n integer matrix matrix. This matrix has the following properties:
- Integers in each row are sorted in ascending from left to right.
- Integers in each column are sorted in ascending from top to bottom.
Example 1:

Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
Output: true
Example 2:
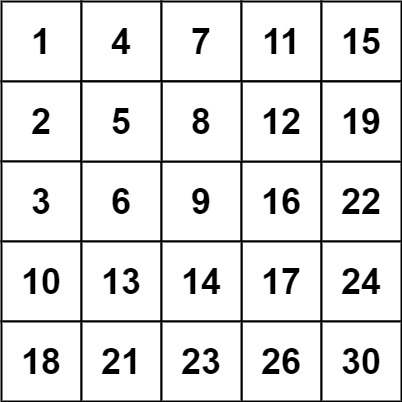
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
Output: false
2. Coding Pattern Used in Solution
The coding pattern used in the C++, Java, and Python implementations is Two Pointers. The algorithm uses two pointers (r and c in C++/Python, row and col in Java) to traverse the matrix from the top-right corner. The movement of the pointers is determined by comparing the current matrix value with the target.
The JavaScript implementation, however, uses a Modified Binary Search pattern. It recursively divides the matrix into smaller submatrices and searches for the target in the relevant sections.
3. Code Implementation in Different Languages
3.1 Search a 2D Matrix II C++
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int m = matrix.size(), n = m ? matrix[0].size() : 0, r = 0, c = n - 1;
while (r < m && c >= 0) {
if (matrix[r][c] == target) {
return true;
}
matrix[r][c] > target ? c-- : r++;
}
return false;
}
};
3.2 Search a 2D Matrix II Java
class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
if(matrix == null || matrix.length < 1 || matrix[0].length <1) {
return false;
}
int col = matrix[0].length-1;
int row = 0;
while(col >= 0 && row <= matrix.length-1) {
if(target == matrix[row][col]) {
return true;
} else if(target < matrix[row][col]) {
col--;
} else if(target > matrix[row][col]) {
row++;
}
}
return false;
}
}
3.3 Search a 2D Matrix II JavaScript
var searchMatrix = function(matrix, target) {
if(!matrix || !matrix.length) return false;
const rows = matrix.length;
const cols = matrix[0].length;
function hasTarget(startRow, endRow, startCol, endCol) {
if(startRow > endRow || startCol > endCol) return false;
const middleRow = Math.floor((endRow - startRow) / 2) + startRow;
const middleCol = Math.floor((endCol - startCol) / 2) + startCol;
if(matrix[middleRow][middleCol] === target) return true;
if (matrix[middleRow][middleCol] < target) {
return hasTarget(middleRow + 1, endRow, startCol, endCol) ||
hasTarget(startRow, middleRow, middleCol + 1, endCol);
} else {
return hasTarget(startRow, endRow, startCol, middleCol - 1) ||
hasTarget(startRow, middleRow - 1, middleCol, endCol);
}
}
return hasTarget(0, rows - 1, 0, cols - 1);
}
3.4 Search a 2D Matrix II Python
class Solution(object):
def searchMatrix(self, matrix, target):
y, i, j = len(matrix), 0, len(matrix[0]) - 1
while i < y and ~j:
cell = matrix[i][j]
if cell == target: return True
elif cell > target: j -= 1
else: i += 1
return False
4. Time and Space Complexity
| Time Complexity | Space Complexity | |
| C++ | O(m + n) | O(1) |
| Java | O(m + n) | O(1) |
| JavaScript | O((m * n) log(min(m, n))) | O(log(min(m, n))) |
| Python | O(m + n) | O(1) |