Last updated on January 5th, 2025 at 01:12 am

Here, we see the Populating Next Right Pointers in Each Node II LeetCode Solution. This Leetcode problem is solved using different approaches in many programming languages, such as C++, Java, JavaScript, Python, etc.

List of all LeetCode Solution

Topics

Depth-First Search, Tree

Companies

Bloomberg, Facebook, Microsoft

Level of Question

Tree

Populating Next Right Pointers in Each Node II LeetCode Solution

1. Problem Statement

Given a binary treestruct Node { int val; Node *left; Node *right; Node *next; }

Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.

Initially, all next pointers are set to NULL.

Example 1:

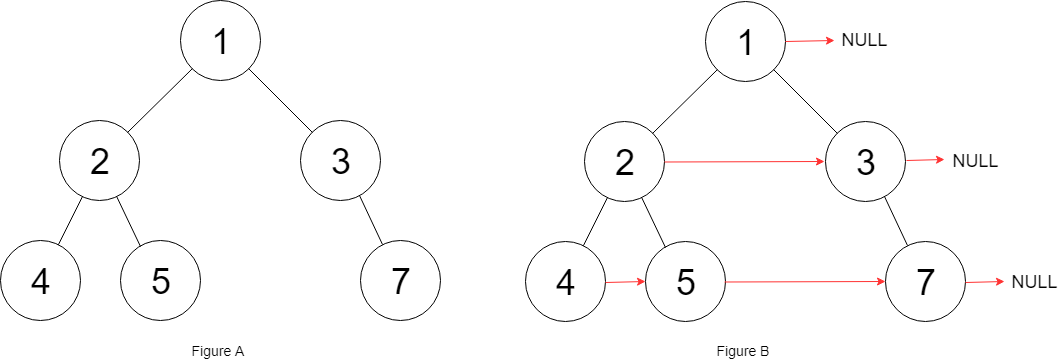
Input: root = [1,2,3,4,5,null,7]
Output: [1,#,2,3,#,4,5,7,#]
Explanation: Given the above binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with ‘#’ signifying the end of each level.

Example 2:
Input: root = []
Output: []

2. Coding Pattern Used in Solution

The coding pattern used in all the provided implementations is Tree Breadth-First Search (BFS). This pattern is used to traverse a tree level by level, connecting nodes at the same level. The BFS approach is evident in the Java, JavaScript, and Python implementations, where a queue is used to process nodes level by level. The C++ implementation, while not explicitly using a queue, also processes nodes level by level, making it conceptually similar to BFS.

3. Code Implementation in Different Languages

3.1 Populating Next Right Pointers in Each Node II C++

class Solution {
public:
    Node* connect(Node* root) {
        Node *currParent = root, *baseChild, *currChild, *nextChild;
        while (currParent) {
            while (currParent->next && !currParent->left && !currParent->right) currParent = currParent->next;
            currChild = baseChild = currParent->left ? currParent->left : currParent->right;
            while (currChild) {
                if (currParent->right && currChild != currParent->right) nextChild = currParent->right;
                else {
                    currParent = currParent->next;
                    while (currParent && !currParent->left && !currParent->right) currParent = currParent->next;
                    nextChild = currParent ? currParent->left ? currParent->left : currParent->right : currParent;
                }
                currChild->next = nextChild;
                currChild = nextChild;
            }
            currParent = baseChild;
        }
        return root;
    }
};

3.2 Populating Next Right Pointers in Each Node II Java

class Solution {
    public Node connect(Node root) {
        if (root == null) {
            return root;
        }
        Queue<Node> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            int levelCount = queue.size();
            Node prev = null;
            for (int i = 0; i < levelCount; i++) {
                Node curNode = queue.poll();
                if (prev != null) {
                    prev.next = curNode;
                }
                prev = curNode;
                if (curNode.left != null) {
                    queue.add(curNode.left);
                }
                if (curNode.right != null) {
                    queue.add(curNode.right);
                }
            }
        }
        return root;        
    }
}

3.3 Populating Next Right Pointers in Each Node II JavaScript

var connect = function(root) {
    if (!root) return root;
    let queue = [root];
    let tempQueue = [];
    while(queue.length){
        let curr = queue.splice(0, 1)[0];
        let {left, right} = curr;    
        if (left) tempQueue.push(left);
        if (right) tempQueue.push(right);
        if (queue.length === 0){
            curr.next = null;
            queue = tempQueue;
            tempQueue = [];
        }else{
            curr.next = queue[0];
        }
    }
    return root;
};

3.4 Populating Next Right Pointers in Each Node II Python

class Solution(object):
    def connect(self, root):
        if not root:
            return None
        q = deque()
        q.append(root)
        dummy=Node(-999)
        while q:
            length=len(q)
            prev=dummy
            for _ in range(length):
                popped=q.popleft()
                if popped.left:
                    q.append(popped.left)
                    prev.next=popped.left
                    prev=prev.next
                if popped.right:
                    q.append(popped.right)
                    prev.next=popped.right
                    prev=prev.next                
        return root

4. Time and Space Complexity

	Time Complexity	Space Complexity
C++	O(n)	1
Java	O(n)	O(w)
JavaScript	O(n)	O(w)
Python	O(n)	O(w)

where, N is the total number of nodes in the tree and w is the maximum width of the tree.