Last updated on February 3rd, 2025 at 10:31 pm
Here, we see Out of Boundary Paths LeetCode Solution. This Leetcode problem is solved using different approaches in many programming languages, such as C++, Java, JavaScript, Python, etc.
List of all LeetCode Solution
Topics
Depth-First Search, Dynamic Programming
Companies
Baidu
Level of Question
Medium

Out of Boundary Paths LeetCode Solution
Table of Contents
1. Problem Statement
There is an m x n grid with a ball. The ball is initially at the position [startRow, startColumn]. You are allowed to move the ball to one of the four adjacent cells in the grid (possibly out of the grid crossing the grid boundary). You can apply at most maxMove moves to the ball.
Given the five integers m, n, maxMove, startRow, startColumn, return the number of paths to move the ball out of the grid boundary. Since the answer can be very large, return it modulo 109 + 7.
Example 1:
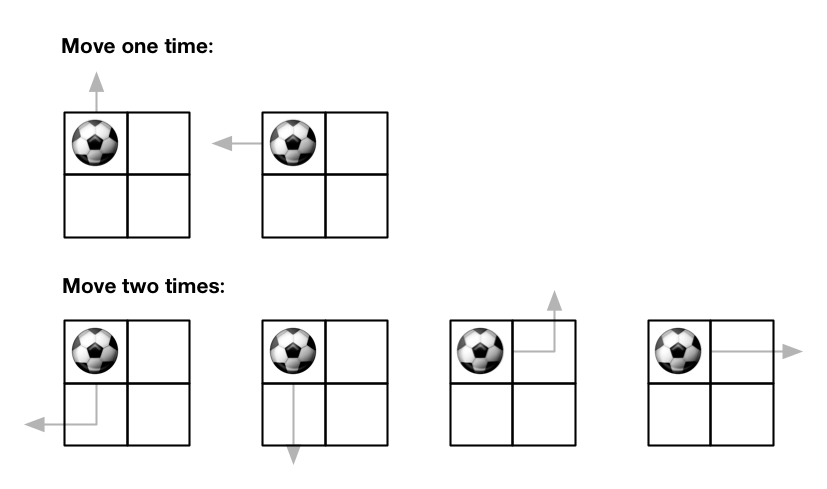
Input: m = 2, n = 2, maxMove = 2, startRow = 0, startColumn = 0
Output: 6
Example 2:
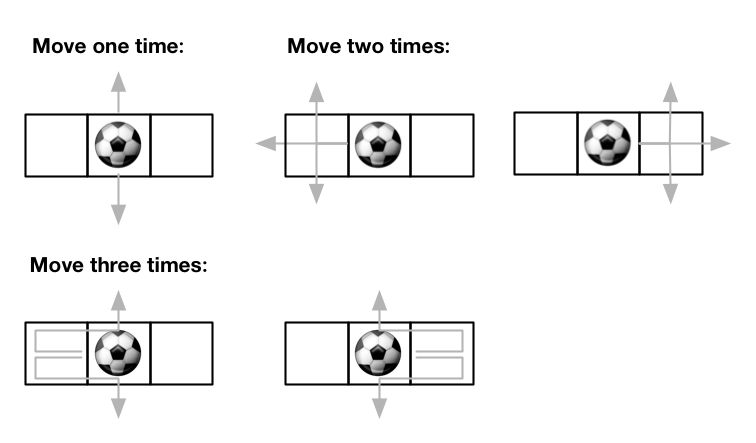
Input: m = 1, n = 3, maxMove = 3, startRow = 0, startColumn = 1
Output: 12
2. Coding Pattern Used in Solution
The coding pattern used in this code is “Dynamic Programming on Grids”. This pattern involves solving problems on a grid (2D matrix) using dynamic programming, where the solution to a problem is built incrementally by reusing previously computed results. This specific problem is a variation of the “Fibonacci Numbers” pattern, as it involves computing results for each cell based on its neighbors in a recursive manner.
3. Code Implementation in Different Languages
3.1 Out of Boundary Paths C++
class Solution {
public:
int findPaths(int m, int n, int maxMove, int startRow, int startColumn) {
const int M = 1000000000 + 7;
vector<vector<int>> dp(m, vector<int>(n, 0));
dp[startRow][startColumn] = 1;
int count = 0;
for (int moves = 1; moves <= maxMove; moves++) {
vector<vector<int>> temp(m, vector<int>(n, 0));
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (i == m - 1) count = (count + dp[i][j]) % M;
if (j == n - 1) count = (count + dp[i][j]) % M;
if (i == 0) count = (count + dp[i][j]) % M;
if (j == 0) count = (count + dp[i][j]) % M;
temp[i][j] = (
((i > 0 ? dp[i - 1][j] : 0) + (i < m - 1 ? dp[i + 1][j] : 0)) % M +
((j > 0 ? dp[i][j - 1] : 0) + (j < n - 1 ? dp[i][j + 1] : 0)) % M
) % M;
}
}
dp = temp;
}
return count;
}
};
3.2 Out of Boundary Paths Java
class Solution {
public int findPaths(int m, int n, int maxMove, int startRow, int startColumn) {
final int M = 1000000000 + 7;
int[][] dp = new int[m][n];
dp[startRow][startColumn] = 1;
int count = 0;
for (int moves = 1; moves <= maxMove; moves++) {
int[][] temp = new int[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (i == m - 1) count = (count + dp[i][j]) % M;
if (j == n - 1) count = (count + dp[i][j]) % M;
if (i == 0) count = (count + dp[i][j]) % M;
if (j == 0) count = (count + dp[i][j]) % M;
temp[i][j] = (
((i > 0 ? dp[i - 1][j] : 0) + (i < m - 1 ? dp[i + 1][j] : 0)) % M +
((j > 0 ? dp[i][j - 1] : 0) + (j < n - 1 ? dp[i][j + 1] : 0)) % M
) % M;
}
}
dp = temp;
}
return count;
}
}
3.3 Out of Boundary Paths JavaScript
var findPaths = function(m, n, maxMove, startRow, startColumn) {
const M = 1000000000 + 7;
let dp = new Array(m).fill(0).map(() => new Array(n).fill(0));
dp[startRow][startColumn] = 1;
let count = 0;
for (let moves = 1; moves <= maxMove; moves++) {
let temp = new Array(m).fill(0).map(() => new Array(n).fill(0));
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
if (i === m - 1) count = (count + dp[i][j]) % M;
if (j === n - 1) count = (count + dp[i][j]) % M;
if (i === 0) count = (count + dp[i][j]) % M;
if (j === 0) count = (count + dp[i][j]) % M;
temp[i][j] = (
((i > 0 ? dp[i - 1][j] : 0) + (i < m - 1 ? dp[i + 1][j] : 0)) % M +
((j > 0 ? dp[i][j - 1] : 0) + (j < n - 1 ? dp[i][j + 1] : 0)) % M
) % M;
}
}
dp = temp;
}
return count;
};
3.4 Out of Boundary Paths Python
class Solution(object):
def findPaths(self, m, n, maxMove, startRow, startColumn):
M = 1000000000 + 7
dp = [[0] * n for _ in range(m)]
dp[startRow][startColumn] = 1
count = 0
for moves in range(1, maxMove + 1):
temp = [[0] * n for _ in range(m)]
for i in range(m):
for j in range(n):
if i == m - 1:
count = (count + dp[i][j]) % M
if j == n - 1:
count = (count + dp[i][j]) % M
if i == 0:
count = (count + dp[i][j]) % M
if j == 0:
count = (count + dp[i][j]) % M
temp[i][j] = (
((dp[i - 1][j] if i > 0 else 0) + (dp[i + 1][j] if i < m - 1 else 0)) % M +
((dp[i][j - 1] if j > 0 else 0) + (dp[i][j + 1] if j < n - 1 else 0)) % M
) % M
dp = temp
return count
4. Time and Space Complexity
| Time Complexity | Space Complexity | |
| C++ | O(maxMove * m * n) | O(m * n) |
| Java | O(maxMove * m * n) | O(m * n) |
| JavaScript | O(maxMove * m * n) | O(m * n) |
| Python | O(maxMove * m * n) | O(m * n) |
- The code uses Dynamic Programming on Grids to solve the problem efficiently.
- It iteratively updates the
dptable for each move, ensuring that the solution is built incrementally. - The time complexity depends on the number of moves (
maxMove) and the size of the grid (m * n), while the space complexity is proportional to the size of the grid.