Last updated on January 5th, 2025 at 11:59 pm

Here, we see a Most Frequent Subtree Sum LeetCode Solution. This Leetcode problem is solved using different approaches in many programming languages, such as C++, Java, JavaScript, Python, etc.

List of all LeetCode Solution

Topics

Hash Table, Tree

Companies

Amazon

Level of Question

Medium

Most Frequent Subtree Sum LeetCode Solution

1. Problem Statement

Given the root of a binary tree, return the most frequent subtree sum. If there is a tie, return all the values with the highest frequency in any order.

The subtree sum of a node is defined as the sum of all the node values formed by the subtree rooted at that node (including the node itself).

Example 1:

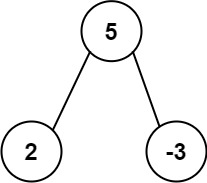
Input: root = [5,2,-3]
Output: [2,-3,4]

Example 2:

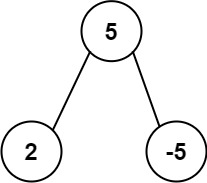
Input: root = [5,2,-5]
Output: [2]

2. Coding Pattern Used in Solution

The coding pattern used in this code is Tree Depth First Search (DFS). The problem involves traversing a binary tree in a post-order manner (left, right, root) to calculate the sum of all subtree nodes and track the frequency of these sums. This traversal is a classic example of DFS.

3. Code Implementation in Different Languages

3.1 Most Frequent Subtree Sum C++

class Solution {
public:
    int solve(TreeNode* root,unordered_map<int,int> &mp,int& x){
        if(root ==NULL)return 0;
        int l = solve(root->left,mp,x);
        int r = solve(root->right,mp,x);
        x = max(x,++mp[root->val+l+r]);
        return root->val+l+r;
    }
    vector<int> findFrequentTreeSum(TreeNode* root) {
        int x = -1;
        unordered_map<int,int> mp;
        solve(root,mp,x);
        vector<int> ans;
        for(auto &i: mp){
            if(i.second == x){
                ans.push_back(i.first);
            }
        }
        return ans;
    }
};

3.2 Most Frequent Subtree Sum Java

class Solution {
    Map<Integer,Integer> map = new HashMap();
    int mostFreq = 0;
    
    public int[] findFrequentTreeSum(TreeNode root) {
        postorder(root);
        ArrayList<Integer> temp = new ArrayList();
        for(int i : map.keySet()){
            if(map.get(i) == mostFreq)temp.add(i); 
        }
        int []res = new int[temp.size()];
        for(int i = 0;i< temp.size();i++){
            res[i] = temp.get(i);
        }
        return res;
    }

    public int postorder(TreeNode root){
        if(root == null)return 0;
        int left = postorder(root.left);
        int right = postorder(root.right);      
        int sum = left + right + root.val;
        map.put(sum,map.getOrDefault(sum,0) + 1);
        mostFreq = Math.max(mostFreq,map.get(sum));
        return sum;
    }
}

3.3 Most Frequent Subtree Sum JavaScript

var findFrequentTreeSum = function(root) {
    const counts = {};
    const max = { val: -Infinity };
    dfs(root, counts, max);
    const sums = [];
    for (let key in counts) {
        if (counts[key] === max.val) sums.push(parseInt(key));
    }
    return sums;
};

function dfs(root, counts, max) {
    if (!root) return 0;
    let sum = root.val + dfs(root.left, counts, max) + dfs(root.right, counts, max);
    counts[sum] = (counts[sum] || 0) + 1;
    max.val = Math.max(max.val, counts[sum]);
    return sum;
}

3.4 Most Frequent Subtree Sum Python

class Solution(object):
    def findFrequentTreeSum(self, root):
        freq = Counter()
        def subtree_sum(node):
            if not node:
                return 0
            s = node.val + subtree_sum(node.left) + subtree_sum(node.right)
            freq[s] += 1
            return s
        subtree_sum(root)
        max_freq = max(freq.values())
        return [s for s in freq if freq[s] == max_freq]

4. Time and Space Complexity

	Time Complexity	Space Complexity
C++	O(n)	O(n)
Java	O(n)	O(n)
JavaScript	O(n)	O(n)
Python	O(n)	O(n)