Last updated on February 9th, 2025 at 07:15 am
Here, we see the Minimum Height Trees LeetCode Solution. This Leetcode problem is solved using different approaches in many programming languages, such as C++, Java, JavaScript, Python, etc.
List of all LeetCode Solution
Topics
Breadth-First Search, Graph
Companies
Level of Question
Medium

Minimum Height Trees LeetCode Solution
Table of Contents
1. Problem Statement
A tree is an undirected graph in which any two vertices are connected by exactly one path. In other words, any connected graph without simple cycles is a tree.
Given a tree of n nodes labelled from 0 to n – 1, and an array of n – 1 edges where edges[i] = [ai, bi] indicates that there is an undirected edge between the two nodes ai and bi in the tree, you can choose any node of the tree as the root. When you select a node x as the root, the result tree has height h. Among all possible rooted trees, those with minimum height (i.e. min(h)) are called minimum height trees (MHTs).
Return a list of all MHTs’ root labels. You can return the answer in any order.
The height of a rooted tree is the number of edges on the longest downward path between the root and a leaf.
Example 1:
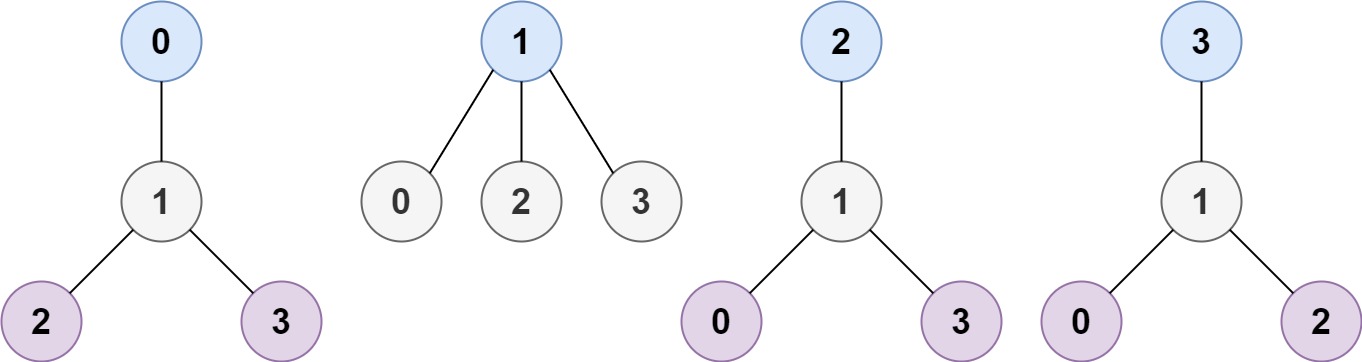
Input: n = 4, edges = [[1,0],[1,2],[1,3]]
Output: [1]
Explanation: As shown, the height of the tree is 1 when the root is the node with label 1 which is the only MHT.
Example 2:
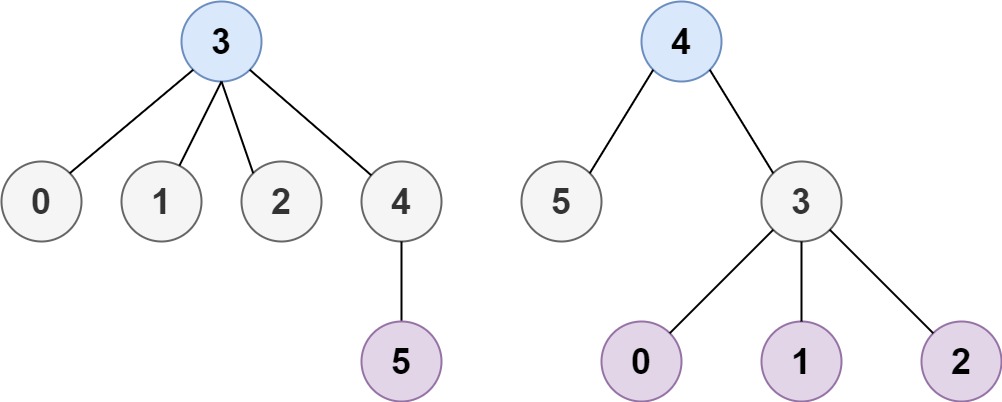
Input: n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]
Output: [3,4]
2. Coding Pattern Used in Solution
The coding pattern used in this code is Tree Breadth-First Search (BFS). The algorithm involves iteratively removing the leaves of the tree (nodes with only one connection) until only the root(s) of the Minimum Height Tree (MHT) remain. This is a classic BFS approach where we process nodes level by level.
3. Code Implementation in Different Languages
3.1 Minimum Height Trees C++
class Solution {
public:
vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {
vector<vector<int>> graph(n);
vector<int> indegree(n, 0), ans;
for(auto &e : edges){
graph[e[0]].push_back(e[1]);
graph[e[1]].push_back(e[0]);
indegree[e[0]]++;
indegree[e[1]]++;
}
queue<int> q;
for(int i=0; i<n;i++){
if(indegree[i]==1) q.push(i), indegree[i]--;
}
while(!q.empty()){
int s = q.size();
ans.clear();
for(int i=0; i<s;i++){
int curr = q.front(); q.pop();
ans.push_back(curr);
for(auto child : graph[curr]){
indegree[child]--;
if(indegree[child]==1) q.push(child);
}
}
}
if(n==1) ans.push_back(0);
return ans;
}
};
3.2 Minimum Height Trees Java
class Solution {
public List<Integer> findMinHeightTrees(int n, int[][] edges) {
if (n == 1) return Collections.singletonList(0);
List<Set<Integer>> adj = new ArrayList<>(n);
for (int i = 0; i < n; ++i) adj.add(new HashSet<>());
for (int[] edge : edges) {
adj.get(edge[0]).add(edge[1]);
adj.get(edge[1]).add(edge[0]);
}
List<Integer> leaves = new ArrayList<>();
for (int i = 0; i < n; ++i)
if (adj.get(i).size() == 1) leaves.add(i);
while (n > 2) {
n -= leaves.size();
List<Integer> newLeaves = new ArrayList<>();
for (int i : leaves) {
int j = adj.get(i).iterator().next();
adj.get(j).remove(i);
if (adj.get(j).size() == 1) newLeaves.add(j);
}
leaves = newLeaves;
}
return leaves;
}
}
3.3 Minimum Height Trees JavaScript
var findMinHeightTrees = function(n, edges) {
if (!edges || n < 2) return [0];
let graph = [];
for (let [x, y] of edges) {
graph[x] = graph[x] || [];
graph[y] = graph[y] || [];
graph[x].push(y);
graph[y].push(x);
}
let leaves = [];
graph.map((pts,i) => pts.length === 1 && leaves.push(i));
while (n > 2) {
n = n - leaves.length;
let nxt_leaves = [];
for (let leave of leaves) {
tmp = graph[leave].pop();
graph[tmp].splice(graph[tmp].indexOf(leave),1);
graph[tmp].length === 1 && nxt_leaves.push(tmp);
}
leaves = nxt_leaves;
}
return leaves;
};
3.4 Minimum Height Trees Python
class Solution(object):
def findMinHeightTrees(self, n, edges):
if n == 1: return [0]
adj = [set() for _ in xrange(n)]
for i, j in edges:
adj[i].add(j)
adj[j].add(i)
leaves = [i for i in xrange(n) if len(adj[i]) == 1]
while n > 2:
n -= len(leaves)
newLeaves = []
for i in leaves:
j = adj[i].pop()
adj[j].remove(i)
if len(adj[j]) == 1: newLeaves.append(j)
leaves = newLeaves
return leaves
4. Time and Space Complexity
| Time Complexity | Space Complexity | |
| C++ | O(V + E) | O(V + E) |
| Java | O(V + E) | O(V + E) |
| JavaScript | O(V + E) | O(V + E) |
| Python | O(V + E) | O(V + E) |
Here:V is the number of nodes (vertices).E is the number of edges.
- Tree Breadth-First Search: The algorithm uses BFS to process nodes level by level, trimming leaves until the root(s) of the MHT are found.
- Graph Representation: The adjacency list is used to represent the tree efficiently.
- Iterative Leaf Removal: By removing leaves iteratively, the algorithm ensures that the remaining nodes are the ones with the minimum height.