Last updated on March 9th, 2025 at 10:24 pm

Here, we see a Maximal Square LeetCode Solution. This Leetcode problem is solved using different approaches in many programming languages, such as C++, Java, JavaScript, Python, etc.

List of all LeetCode Solution

Topics

Dynamic Programming

Companies

Airbnb, Apple, Facebook

Level of Question

Medium

Maximal Square LeetCode Solution

1. Problem Statement

Given an m x n binary matrix filled with 0’s and 1’s, find the largest square containing only 1’s and return its area.

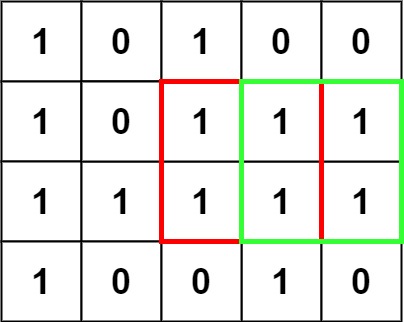
Example 1: (fig-1)
Input: matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
Output: 4

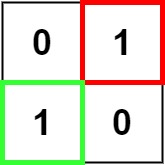
Example 2: (fig-2)
Input: matrix = [["0","1"],["1","0"]]
Output: 1

Example 3:
Input: matrix = [["0"]]
Output: 0

2. Coding Pattern Used in Solution

The coding pattern used in this problem is Dynamic Programming (DP). Specifically, it is a 2D DP problem where the solution builds upon previously computed subproblems to find the maximal square of ‘1’s in a binary matrix.

3. Code Implementation in Different Languages

3.1 Maximal Square C++

class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        if (matrix.empty()) {
            return 0;
        }
        int m = matrix.size(), n = matrix[0].size(), sz = 0;
        vector<vector<int>> dp(m, vector<int>(n, 0));
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (!i || !j || matrix[i][j] == '0') {
                    dp[i][j] = matrix[i][j] - '0';
                } else {
                    dp[i][j] = min(dp[i - 1][j - 1], min(dp[i - 1][j], dp[i][j - 1])) + 1;
                }
                sz = max(dp[i][j], sz);
            }
        }
        return sz * sz;
    }
};

3.2 Maximal Square Java

class Solution {
    public int maximalSquare(char[][] matrix) {
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0)
    return 0;
      
  int max = 0, n = matrix.length, m = matrix[0].length;
  int[][] dp = new int[n + 1][m + 1];
  
  for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= m; j++) {
      if (matrix[i - 1][j - 1] == '1') {
        dp[i][j] = Math.min(dp[i - 1][j - 1], Math.min(dp[i - 1][j], dp[i][j - 1])) + 1;
        max = Math.max(max, dp[i][j]);
      }
    }
  }
  return max * max;
    }
}

3.3 Maximal Square JavaScript

var maximalSquare = function(matrix) {
    let max = 0
  for (let i = 0; i < matrix.length; i++) {
    for (let j = 0; j < matrix[0].length; j++) {
      if (matrix[i][j] === "0") continue
      if(i > 0 && j > 0)
        matrix[i][j] = Math.min(matrix[i - 1][j], matrix[i][j - 1], matrix[i - 1][j - 1]) + 1
      max = Math.max(matrix[i][j], max)
    }
  }
  return max ** 2
};

3.4 Maximal Square Python

class Solution(object):
    def maximalSquare(self, matrix):
        if matrix is None or len(matrix) < 1:
            return 0
        
        rows = len(matrix)
        cols = len(matrix[0])
        
        dp = [[0]*(cols+1) for _ in range(rows+1)]
        max_side = 0
        
        for r in range(rows):
            for c in range(cols):
                if matrix[r][c] == '1':
                    dp[r+1][c+1] = min(dp[r][c], dp[r+1][c], dp[r][c+1]) + 1
                    max_side = max(max_side, dp[r+1][c+1])
                
        return max_side * max_side

4. Time and Space Complexity

	Time Complexity	Space Complexity
C++	O(m * n)	O(m * n)
Java	O(m * n)	O(m * n)
JavaScript	O(m * n)	O(1)
Python	O(m * n)	O(m * n)

1. The JavaScript implementation modifies the input matrix in-place, which reduces the space complexity to O(1). However, this approach may not be suitable if the input matrix cannot be modified.
2. The C++, Java, and Python implementations use an additional 2D DP table, resulting in a space complexity of O(m * n).
3. All implementations have the same time complexity of O(m * n), as they iterate through the matrix once.