Last updated on January 5th, 2025 at 12:39 am

Here, we see the Lowest Common Ancestor of a Binary Search Tree LeetCode Solution. This Leetcode problem is solved using different approaches in many programming languages, such as C++, Java, JavaScript, Python, etc.

List of all LeetCode Solution

Topics

Tree

Companies

Amazon, Facebook, Microsoft, Twitter

Level of Question

Medium

Lowest Common Ancestor of a Binary Search Tree LeetCode Solution

1. Problem Statement

Given a binary search tree (BST), find the lowest common ancestor (LCA) node of two given nodes in the BST.

According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”

Example 1:

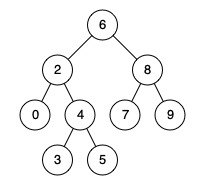
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
Output: 6
Explanation: The LCA of nodes 2 and 8 is 6.

Example 2:

Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
Output: 2
Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.

Example 3:
Input: root = [2,1], p = 2, q = 1
Output: 2

2. Coding Pattern Used in Solution

The coding pattern used in this code is “Tree Depth First Search (DFS)”. The code traverses the binary search tree (BST) recursively (or iteratively in the JavaScript version) to find the lowest common ancestor (LCA) of two nodes. The traversal is depth-first because it explores one branch of the tree fully before moving to another branch.

3. Code Implementation in Different Languages

3.1 Lowest Common Ancestor of a Binary Search Tree C++

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root==NULL) return nullptr;
        if(root->val>p->val&&root->val>q->val) return lowestCommonAncestor(root->left,p,q);
        if(root->val<p->val&&root->val<q->val) return lowestCommonAncestor(root->right,p,q);
        return root;         
    }
};

3.2 Lowest Common Ancestor of a Binary Search Tree Java

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root==null) return null;
        if(p.val<root.val&&q.val<root.val) {
            return lowestCommonAncestor(root.left,p,q);
        }
        else if(p.val>root.val&&q.val>root.val){
            return lowestCommonAncestor(root.right,p,q);
        }
        else
        return root;        
    }
}

3.3 Lowest Common Ancestor of a Binary Search Tree JavaScript

var lowestCommonAncestor = function(root, p, q) {
    while (root) {
        if (root.val < p.val && root.val < q.val) {
            root = root.right;
        }
        else if (root.val > p.val && root.val > q.val) {
            root = root.left;
        } else {
            break;
        }
    }
    return root;    
};

3.4 Lowest Common Ancestor of a Binary Search Tree Python

class Solution(object):
    def lowestCommonAncestor(self, root, p, q):
        if root:
            if root.val > p.val and root.val > q.val:
                return self.lowestCommonAncestor(root.left, p, q)
            elif root.val < p.val and root.val < q.val:
                return self.lowestCommonAncestor(root.right, p, q)
            else:
                return root

4. Time and Space Complexity

	Time Complexity(Balanced Tree)	Time Complexity(Unbalanced Tree)	Space Complexity(Balanced Tree)	Space Complexity (Unbalanced Tree)
C++	`O(log N)`	`O(N)`	`O(log N)`	`O(N)`
Java	`O(log N)`	`O(N)`	`O(log N)`	`O(N)`
JavaScript	`O(log N)`	`O(N)`	`O(1)`	`O(1)`
Python	`O(log N)`	`O(N)`	`O(log N)`	`O(N)`