Last updated on March 1st, 2025 at 10:15 pm
Here, we see a Kth Smallest Number in Multiplication Table LeetCode Solution. This Leetcode problem is solved using different approaches in many programming languages, such as C++, Java, JavaScript, Python, etc.
List of all LeetCode Solution
Topics
Companies
Level of Question
Hard

Kth Smallest Number in Multiplication Table LeetCode Solution
Table of Contents
1. Problem Statement
Nearly everyone has used the Multiplication Table. The multiplication table of size m x n is an integer matrix mat where mat[i][j] == i * j (1-indexed).
Given three integers m, n, and k, return the kth smallest element in the m x n multiplication table.
Example 1:
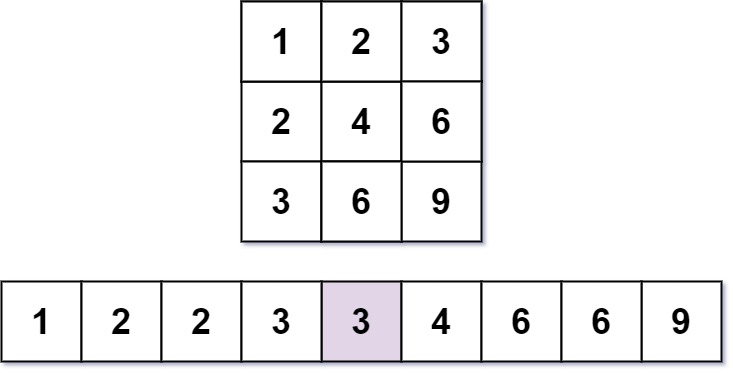
Input: m = 3, n = 3, k = 5
Output: 3
Explanation: The 5th smallest number is 3.
Example 2:
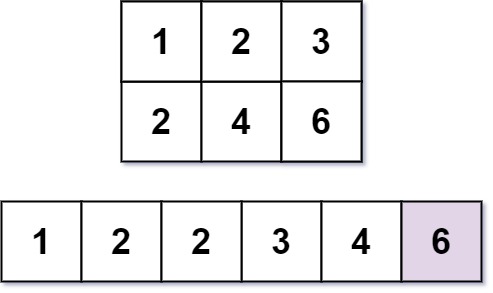
Input: m = 2, n = 3, k = 6
Output: 6
Explanation: The 6th smallest number is 6.
2. Coding Pattern Used in Solution
The coding pattern used in all the provided implementations is Modified Binary Search. This pattern is used to efficiently search for a specific value or condition in a sorted or bounded range by repeatedly dividing the search space in half. In this case, the problem involves finding the kth smallest number in a multiplication table, and the binary search is applied to narrow down the range of possible values.
3. Code Implementation in Different Languages
3.1 Kth Smallest Number in Multiplication Table C++
class Solution {
public:
int findKthNumber(int m, int n, int k) {
int l=1, L=m*n;
while (L) {
int d=L>>1;
int x=l+d;
int y=0;
for (int a=n, b=0; a>0; --a) {
while (b<=m and a*b<=x) ++b;
y+=b-1;
}
if (y<k) {
l=x+1;
L-=d+1;
} else
L=d;
}
return l;
}
};
3.2 Kth Smallest Number in Multiplication Table Java
class Solution {
public int countlessthanmid(int n ,int m, int mid){
int count=0;
int i=1;
int j =m;
while(i<=n && j>=1){
if(i*j<=mid){
count+=j;
i++;
}else{
j--;
}
}
return count;
}
public int findKthNumber(int m, int n, int k) {
int l = 1;
int h = m*n;
int mid =0;
int res = 0;
while(l<=h){
mid = l+(h-l)/2;
int count = countlessthanmid(m, n, mid);
if(count<k){
l = mid+1;
}else{
res = mid;
h = mid-1;
}
}
return res;
}
}
3.3 Kth Smallest Number in Multiplication Table JavaScript
var findKthNumber = function (m, n, k) {
let low = 0, high = m * n;
while (low + 1 < high) {
let mid = low + ~~((high - low) / 2);
let count = lessThanEqual(mid, m, n);
if (count >= k) high = mid;
else low = mid;
}
return high;
};
function lessThanEqual(target, rows, cols) {
let count = 0;
for (let i = 1; i <= rows; i++) {
count += Math.min(~~(target / i), cols);
}
return count;
}
3.4 Kth Smallest Number in Multiplication Table Python
class Solution(object):
def findKthNumber(self, m, n, k):
def enough(m, n, x, a):
cnt = 0
for i in range(1, m + 1):
cnt += min(x // i, n)
return cnt >= a
l, r = 0, m * n
while l < r:
mid = l + (r - l) // 2
if enough(m, n, mid, k):
r = mid
else:
l = mid + 1
return l
4. Time and Space Complexity
| Time Complexity | Space Complexity | |
| C++ | O(m * log(m * n)) | O(1) |
| Java | O(m * log(m * n)) | O(1) |
| JavaScript | O(m * log(m * n)) | O(1) |
| Python | O(m * log(m * n)) | O(1) |
- The problem is solved using Modified Binary Search to efficiently find the
kth smallest number in a multiplication table. - The helper function counts how many numbers are less than or equal to a given value (
mid) in the table. - The time complexity is O(m * log(m * n)), and the space complexity is O(1) for all implementations.