Last updated on January 9th, 2025 at 03:33 am

Here, we see a Guess Number Higher or Lower II LeetCode Solution. This Leetcode problem is solved using different approaches in many programming languages, such as C++, Java, JavaScript, Python, etc.

List of all LeetCode Solution

Topics

Dynamic Programming, Minimax

Companies

Google

Level of Question

Medium

Guess Number Higher or Lower II LeetCode Solution

1. Problem Statement

We are playing the Guessing Game. The game will work as follows:

I pick a number between 1 and n.
You guess a number.
If you guess the right number, you win the game.
If you guess the wrong number, then I will tell you whether the number I picked is higher or lower, and you will continue guessing.
Every time you guess a wrong number x, you will pay x dollars. If you run out of money, you lose the game.

Given a particular n, return the minimum amount of money you need to guarantee a win regardless of what number I pick.

Example 1:

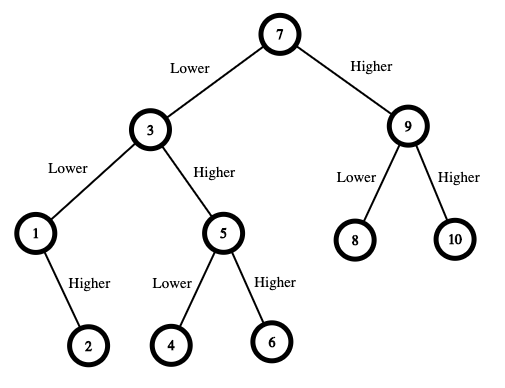
Input: n = 10
Output: 16

Explanation: The winning strategy is as follows:
– The range is [1,10]. Guess 7.
– If this is my number, your total is $0. Otherwise, you pay $7.
– If my number is higher, the range is [8,10]. Guess 9.
– If this is my number, your total is $7. Otherwise, you pay $9.
– If my number is higher, it must be 10. Guess 10. Your total is $7 + $9 = $16.

– If my number is lower, it must be 8. Guess 8. Your total is $7 + $9 = $16.
– If my number is lower, the range is [1,6]. Guess 3.
– If this is my number, your total is $7. Otherwise, you pay $3.
– If my number is higher, the range is [4,6]. Guess 5.
– If this is my number, your total is $7 + $3 = $10. Otherwise, you pay $5.

– If my number is higher, it must be 6. Guess 6. Your total is $7 + $3 + $5 = $15.
– If my number is lower, it must be 4. Guess 4. Your total is $7 + $3 + $5 = $15.
– If my number is lower, the range is [1,2]. Guess 1.
– If this is my number, your total is $7 + $3 = $10. Otherwise, you pay $1.
– If my number is higher, it must be 2. Guess 2. Your total is $7 + $3 + $1 = $11. The worst case in all these scenarios is that you pay $16. Hence, you only need $16 to guarantee a win.

Example 2:
Input: n = 1
Output: 0
Explanation: There is only one possible number, so you can guess 1 and not have to pay anything.

Example 3:
Input: n = 2
Output: 1
Explanation: There are two possible numbers, 1 and 2.
– Guess 1.
– If this is my number, your total is $0. Otherwise, you pay $1.
– If my number is higher, it must be 2. Guess 2. Your total is $1. The worst case is that you pay $1.

2. Coding Pattern Used in Solution

The coding pattern used in all the provided implementations is Dynamic Programming (DP). Specifically, this problem is a variation of the “0/1 Knapsack” pattern, where we are trying to minimize the maximum cost (or risk) of guessing a number in a range. The problem involves breaking the problem into smaller subproblems (ranges of numbers) and solving them optimally using a bottom-up or top-down approach.

3. Code Implementation in Different Languages

3.1 Guess Number Higher or Lower II C++

class Solution {
public:
    int getMoneyAmount(int n) {
        vector<vector<int>> dp(n+1, vector<int>(n+1, 0));
        for(int len=2; len<=n; ++len){
            for(int begin=0; begin<=n-len; ++begin){
                int end = begin + len;
                for(int i=begin; i<end; ++i){
                    int numPicked = i+1;
                    if(i == begin){
                        dp[begin][end] = numPicked + dp[begin+1][end];
                    } else {
                        dp[begin][end] = min(dp[begin][end], max(dp[begin][i], dp[i+1][end]) + numPicked);
                    }
                }
            }
        }
        return dp[0][n];
    }
};

3.2 Guess Number Higher or Lower II Java

class Solution {
    public int getMoneyAmount(int n) {
	    int[][] f = new int[n + 1][n + 1];
	    Deque<Integer[]> q;
	    int a, b, k0, v, f1, f2;
	    for (b = 2; b <= n; b++) {
		    k0 = b - 1;
		    q = new LinkedList<Integer[]>();
		    for (a = b - 1; a > 0; a--) {
                while (f[a][k0 - 1] > f[k0 + 1][b])
                    k0--;
                while (!q.isEmpty() && q.peekFirst()[0] > k0)
                    q.pollFirst();
                v = f[a + 1][b] + a;
                while (!q.isEmpty() && v < q.peekLast()[1])
                    q.pollLast();
                q.offerLast(new Integer[] { a, v });
                f1 = q.peekFirst()[1];
                f2 = f[a][k0] + k0 + 1;
                f[a][b] = Math.min(f1, f2);
            }
        }
        return f[1][n];
    }
}

3.3 Guess Number Higher or Lower II JavaScript

var getMoneyAmount = function (n) {
  const dp = Array(n + 1).fill(null).map(() => Array(n + 1).fill(Infinity))
  const minimax = (l, r) => {
    if (l >= r) return 0
    if (dp[l][r] !== Infinity) return dp[l][r]
    for (let i = l; i <= r; i++) {
      dp[l][r] = Math.min(dp[l][r], i + Math.max(minimax(i + 1, r), minimax(l, i - 1)))
    }
    return dp[l][r]
  }
  return minimax(1, n)
};

3.4 Guess Number Higher or Lower II Python

class Solution(object):
    def getMoneyAmount(self, n):
        need = [[0] * (n+1) for _ in range(n+1)]
        for lo in range(n, 0, -1):
            for hi in range(lo+1, n+1):
                need[lo][hi] = min(x + max(need[lo][x-1], need[x+1][hi])
                                for x in range(lo, hi))
        return need[1][n]

4. Time and Space Complexity

	Time Complexity	Space Complexity
C++	O(n³)	O(n²)
Java	O(n³)	O(n²)
JavaScript	O(n³)	O(n²)
Python	O(n³)	O(n²)

The problem is a minimax problem: minimize the maximum cost.
The DP table is filled iteratively (bottom-up) or recursively (top-down) to solve smaller subproblems first.
The time complexity is cubic due to the nested loops or recursive calls for each range and guess.