Last updated on February 2nd, 2025 at 06:11 am
Here, we see a Game of Life LeetCode Solution. This Leetcode problem is solved using different approaches in many programming languages, such as C++, Java, JavaScript, Python, etc.
List of all LeetCode Solution
Topics
Array
Companies
Dropbox, Google, Snapchat, TwoSigma
Level of Question
Medium

Game of Life LeetCode Solution
Table of Contents
1. Problem Statement
According to Wikipedia’s article: “The Game of Life, also known simply as Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970.”
The board is made up of an m x n grid of cells, where each cell has an initial state: live (represented by a 1) or dead (represented by a 0). Each cell interacts with its eight neighbors (horizontal, vertical, diagonal) using the following four rules (taken from the above Wikipedia article):
- Any live cell with fewer than two live neighbors dies as if caused by under-population.
- Any live cell with two or three live neighbors lives on to the next generation.
- Any live cell with more than three live neighbors dies, as if by over-population.
- Any dead cell with exactly three live neighbors becomes a live cell, as if by reproduction.
The next state is created by applying the above rules simultaneously to every cell in the current state, where births and deaths occur simultaneously. Given the current state of the m x n grid board, return the next state.
Example 1:
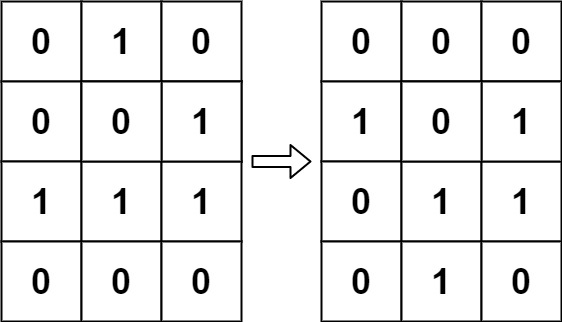
Input: board = [[0,1,0],[0,0,1],[1,1,1],[0,0,0]]
Output: [[0,0,0],[1,0,1],[0,1,1],[0,1,0]]
Example 2:
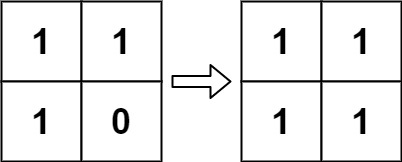
Input: board = [[1,1],[1,0]]
Output: [[1,1],[1,1]]
2. Coding Pattern Used in Solution
The coding pattern used in the provided code is “Matrix Traversal with State Encoding”. This pattern involves traversing a 2D grid (matrix) and encoding additional information into the grid itself to avoid using extra space. The state encoding is achieved by modifying the values in the grid to represent both the current and next states simultaneously.
3. Code Implementation in Different Languages
3.1 Game of Life LeetCode C++
class Solution {
public:
void gameOfLife(vector<vector<int>>& board) {
int m = board.size(), n = m ? board[0].size() : 0;
for (int i=0; i<m; ++i) {
for (int j=0; j<n; ++j) {
int count = 0;
for (int I=max(i-1, 0); I<min(i+2, m); ++I)
for (int J=max(j-1, 0); J<min(j+2, n); ++J)
count += board[I][J] & 1;
if (count == 3 || count - board[i][j] == 3)
board[i][j] |= 2;
}
}
for (int i=0; i<m; ++i)
for (int j=0; j<n; ++j)
board[i][j] >>= 1;
}
};
3.2 Game of Life Java
class Solution {
public void gameOfLife(int[][] board) {
if (board == null || board.length == 0) return;
int m = board.length, n = board[0].length;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
int lives = liveNeighbors(board, m, n, i, j);
if (board[i][j] == 1 && lives >= 2 && lives <= 3) {
board[i][j] = 3;
}
if (board[i][j] == 0 && lives == 3) {
board[i][j] = 2;
}
}
}
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
board[i][j] >>= 1;
}
}
}
public int liveNeighbors(int[][] board, int m, int n, int i, int j) {
int lives = 0;
for (int x = Math.max(i - 1, 0); x <= Math.min(i + 1, m - 1); x++) {
for (int y = Math.max(j - 1, 0); y <= Math.min(j + 1, n - 1); y++) {
lives += board[x][y] & 1;
}
}
lives -= board[i][j] & 1;
return lives;
}
}
3.3 Game of Life JavaScript
var gameOfLife = function(board) {
if(board.length === 0){
return board;
}
var checkNeighbors = function(row, col){
var score = -board[row][col];
var r, c;
for(r = row - 1; r <= row + 1; r++){
for(c = col - 1; c <= col + 1; c++){
if(typeof board[r] !== "undefined" && typeof board[r][c] !== "undefined"){
score += Math.abs(Math.floor(board[r][c]));
}
}
}
return score;
};
var r, c;
for(r = 0; r < board.length; r++){
for(c = 0; c < board[0].length; c++){
var score = checkNeighbors(r, c);
if(board[r][c] === 1){
if(score < 2 || score > 3){
board[r][c] = -0.5;
}
}
else if(board[r][c] === 0){
if(score === 3){
board[r][c] = 0.5;
}
}
}
}
for(r = 0; r < board.length; r++){
for(c = 0; c < board[0].length; c++){
board[r][c] = Math.ceil(board[r][c]);
}
}
};
3.4 Game of Life Python
var gameOfLife = function(board) {
if(board.length === 0){
return board;
}
var checkNeighbors = function(row, col){
var score = -board[row][col];
var r, c;
for(r = row - 1; r <= row + 1; r++){
for(c = col - 1; c <= col + 1; c++){
if(typeof board[r] !== "undefined" && typeof board[r][c] !== "undefined"){
score += Math.abs(Math.floor(board[r][c]));
}
}
}
return score;
};
var r, c;
for(r = 0; r < board.length; r++){
for(c = 0; c < board[0].length; c++){
var score = checkNeighbors(r, c);
if(board[r][c] === 1){
if(score < 2 || score > 3){
board[r][c] = -0.5;
}
}
else if(board[r][c] === 0){
if(score === 3){
board[r][c] = 0.5;
}
}
}
}
for(r = 0; r < board.length; r++){
for(c = 0; c < board[0].length; c++){
board[r][c] = Math.ceil(board[r][c]);
}
}
};
4. Time and Space Complexity
| Time Complexity | Space Complexity | |
| C++ | O(m * n) | O(1) |
| Java | O(m * n) | O(1) |
| JavaScript | O(m * n) | O(1) |
| Python | O(m * n) | O(1) |
where, m is the number of rows in the grid.n is the number of columns in the grid.
- State Encoding: The use of bitwise operations or fractional values to encode the next state is a clever way to save space.
- Matrix Traversal: The grid is traversed twice—once to calculate the next state and once to update the grid.
- In-Place Update: The grid is updated in-place, making the solution space-efficient.