Last updated on March 1st, 2025 at 10:14 pm
Here, we see an Erect the Fence LeetCode Solution. This Leetcode problem is solved using different approaches in many programming languages, such as C++, Java, JavaScript, Python, etc.
List of all LeetCode Solution
Topics
Geometry
Companies
Level of Question
Hard

Erect the Fence LeetCode Solution
Table of Contents
1. Problem Statement
You are given an array trees where trees[i] = [xi, yi] represents the location of a tree in the garden.
Fence the entire garden using the minimum length of rope, as it is expensive. The garden is well-fenced only if all the trees are enclosed.
Return the coordinates of trees that are exactly located on the fence perimeter. You may return the answer in any order.
Example 1:
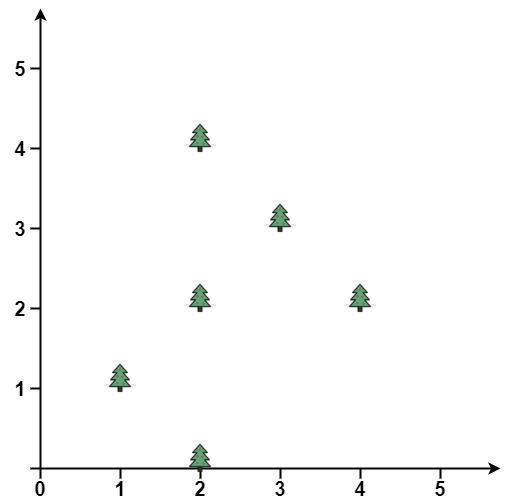
Input: trees = [[1,1],[2,2],[2,0],[2,4],[3,3],[4,2]]
Output: [[1,1],[2,0],[4,2],[3,3],[2,4]]
Explanation: All the trees will be on the perimeter of the fence except the tree at [2, 2], which will be inside the fence.
Example 2:
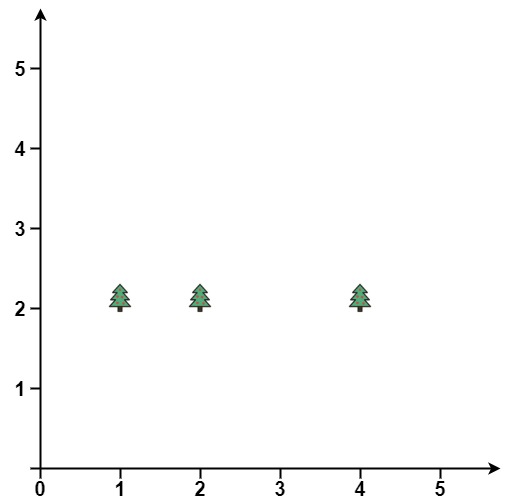
Input: trees = [[1,2],[2,2],[4,2]]
Output: [[4,2],[2,2],[1,2]]
Explanation: The fence forms a line that passes through all the trees.
2. Coding Pattern Used in Solution
The coding pattern used in all the provided implementations is “Convex Hull Algorithm”, specifically Monotone Chain Algorithm (or a variant of it). This pattern is used to find the convex hull of a set of points in a 2D plane, which is the smallest convex polygon that can enclose all the points.
3. Code Implementation in Different Languages
3.1 Erect the Fence C++
class Solution {
public:
int Cross_Product_fun(vector<int> p,vector<int> q,vector<int> r){
int ans = ((q[0]-p[0])*(r[1]-p[1]))-((q[1]-p[1])*(r[0]-p[0]));
return ans;
}
vector<vector<int>> outerTrees(vector<vector<int>>& trees) {
int sz = trees.size();
if(sz<=3){
return trees;
}
else{
sort(trees.begin(),trees.end());
vector<vector<int>> up_hull;
vector<vector<int>> low_hull;
up_hull.push_back(trees[0]);
up_hull.push_back(trees[1]);
for(int j=2;j<sz;j++){
int n = up_hull.size();
while(n>=2 && Cross_Product_fun(up_hull[n-2],up_hull[n-1],trees[j]) > 0){
up_hull.pop_back();
n--;
}
up_hull.push_back(trees[j]);
}
low_hull.push_back(trees[sz-1]);
low_hull.push_back(trees[sz-2]);
for(int j=sz-3;j>=0;j--){
int m = low_hull.size();
while(m>=2 && Cross_Product_fun(low_hull[m-2],low_hull[m-1],trees[j]) > 0){
low_hull.pop_back();
m--;
}
low_hull.push_back(trees[j]);
}
up_hull.insert(up_hull.end(),low_hull.begin(),low_hull.end());
sort(up_hull.begin(),up_hull.end());
up_hull.erase(unique(up_hull.begin(),up_hull.end()),up_hull.end());
return up_hull;
}
}
};
3.2 Erect the Fence Java
class Solution {
public int[][] outerTrees(int[][] trees) {
Arrays.sort(trees, (p1, p2) -> {
if (p1[0] == p2[0]) {
return p2[1] - p1[1];
}
return p1[0] - p2[0];
});
Set<Point> res = new HashSet<>();
res.add(new Point(trees[0]));
int n = trees.length;
int i = 0;
while (i != n - 1) {
double bestSlope = Integer.MIN_VALUE;
int[] nextPoint = trees[i + 1];
int jCandidate = i + 1;
for (int j = i + 1; j < n; j++) {
double slope = calculateSlope(trees[i], trees[j]);
if (slope > bestSlope) {
bestSlope = slope;
nextPoint = trees[j];
jCandidate = j;
}
}
i = jCandidate;
res.add(new Point(nextPoint));
}
i = n - 1;
while (i != 0) {
double bestSlope = Integer.MIN_VALUE;
int[] nextPoint = trees[i - 1];
int jCandidate = i - 1;
for (int j = i - 1; j >= 0; j--) {
double slope = calculateSlope(trees[j], trees[i]);
if (slope > bestSlope) {
bestSlope = slope;
nextPoint = trees[j];
jCandidate = j;
}
}
i = jCandidate;
res.add(new Point(nextPoint));
}
return res.stream().map(p -> new int[]{p.x, p.y}).toArray(int[][]::new);
}
private double calculateSlope(int[] p1, int[] p2) {
if (p1[0] == p2[0]) { // 0 division
return Integer.MIN_VALUE;
}
return (double) (p2[1] - p1[1]) / (double) (p2[0] - p1[0]);
}
private static class Point {
public int x;
public int y;
public Point(int x, int y) {
this.x = x;
this.y = y;
}
public Point(int[] p) {
this.x = p[0];
this.y = p[1];
}
public String toString() {
return "Point{" +
"x=" + x +
", y=" + y +
'}';
}
public boolean equals(Object o) {
if (this == o) return true;
if (o == null || getClass() != o.getClass()) return false;
Point point = (Point) o;
return x == point.x && y == point.y;
}
public int hashCode() {
return Objects.hash(x, y);
}
}
}
3.3 Erect the Fence JavaScript
var outerTrees = function(trees) {
trees.sort((a, b) => a[0] - b[0] == 0 ? a[1] - b[1] : a[0] - b[0])
const cmpSlopes = ([x1, y1], [x2, y2], [x3, y3]) => (y3 - y1) * (x2 - x1) - (y2 - y1) * (x3 - x1)
const higher = []
const lower = []
for (let point of trees) {
while (higher.length > 1 && cmpSlopes(higher[higher.length - 2], higher[higher.length - 1], point) > 0)
higher.pop();
while (lower.length > 1 && cmpSlopes(lower[lower.length - 2], lower[lower.length - 1], point) < 0)
lower.pop();
higher.push(point);
lower.push(point);
}
return [...new Set([...higher, ...lower])];
};
3.4 Erect the Fence Python
class Solution(object):
def outerTrees(self, trees):
def ccw(A, B, C):
return (B[0]-A[0])*(C[1]-A[1]) - (B[1]-A[1])*(C[0]-A[0])
if len(trees) <= 1:
return trees
hull = []
trees.sort()
for i in itertools.chain(range(len(trees)), reversed(range(len(trees)-1))):
while len(hull) >= 2 and ccw(hull[-2], hull[-1], trees[i]) < 0:
hull.pop()
hull.append(trees[i])
hull.pop()
for i in range(1, (len(hull)+1)//2):
if hull[i] != hull[-1]:
break
hull.pop()
return hull
4. Time and Space Complexity
| Time Complexity | Space Complexity | |
| C++ | O(n log n) | O(n) |
| Java | O(n2) | O(n) |
| JavaScript | O(n log n) | O(n) |
| Python | O(n log n) | O(n) |
- The C++, JavaScript, and Python implementations use the Monotone Chain Algorithm, which is more efficient (O(n log n)).
- The Java implementation uses a brute-force slope-based approach, which is less efficient (O(n2)).
- All implementations use a geometric approach to determine the convex hull, leveraging cross products or slopes to decide the inclusion of points in the hull.