Compiler Design Gate Questions

Here, We will see Compiler Design GATE Questions from previous year’s papers and the syllabus of Compiler Design for GATE Exam.

1. Compiler Design in Gate CSE Exam

Compiler Design is a pivotal topic in the GATE Computer Science and Information Technology (CS/IT) exam, focusing on the principles and techniques behind translating high-level programming languages into efficient machine code. This subject tests candidates’ understanding of compiler phases, optimization strategies, and runtime environments, with questions often blending theoretical concepts and practical applications.

2. Compiler Design Syllabus

The syllabus for Compiler Design in GATE CSE includes:

1. Lexical Analysis: Tokenization, finite automata, and regular expressions.
2. Parsing: Context-free grammars, LL(1), LR(1), and LALR parsers.
3. Syntax-Directed Translation: Attribute grammars, intermediate representations (e.g., three-address code).
4. Runtime Environments: Activation records, parameter passing, stack allocation.
5. Intermediate Code Generation & Optimization: Control flow graphs, data-flow analysis (e.g., constant propagation, dead code elimination).
6. Code Generation: Instruction selection, register allocation.

Compiler Design Gate Questions

1. Match the following NFAs with the regular expressions they correspond to
1. ∈ + 0(01*1 + 00)*01*
2. ∈ + 0(10*1 + 00)*0
3. ∈ + 0(10*1 + 10)*1
4. ∈ + 0(10*1 + 10)*10*

1. P-2, Q-1, R-3, S- 4
2. P-1, Q-3, R-2, S- 4
3. P-1, Q-2, R-3, S- 4
4. P-3, Q-2, R-1, S- 4

2. Which of the following are regular sets?
I. {aⁿb^2m | n ≥ 0, m ≥ 0}
II. {aⁿb^m | n = 2m}
III. {aⁿb^m | n ≠ m}
IV. {xcy | x, y ∈ {a, b}*}

1. I and IV only
2. I and III only
3. I only
4. IV only

3. Which one of the following languages over the alphabet {0, 1} is described by the regular expression:(0 + 1)*0(0 + 1)*0(0 + 1)*

1. The set of all strings containing the substring 00.
2. The set of all strings containing atmost two 0’s.
3. The set of all strings containing at least two 0’s.
4. The set of all strings that begin and end with either 0 or 1.

4. Which one of the following is FALSE?

1. There is a unique minimal DFA for every regular language.
2. Every NFA can be converted to an equivalent PDA.
3. Complement of every context-free language isrecursive.
4. Every non-deterministic PDA can be converted to an equivalent deterministic PDA.

5. Match all items in Group 1 with correct options from those given in Group 2

1. P–4, Q–1, R–2, S–3
2. P–3, Q–1, R–4, S–2
3. P–3, Q–4, R–1, S–2
4. P–2, Q–1, R–4, S–3

6. The above DFA accepts the set of all strings over {0, 1} that

1. Begin either with 0 or 1
2. End with 0
3. End with 00
4. Contain the substring 00.

7. Let L = {w ∈ (0 + 1)* | w has even number of 1’s}, i.e., L is the set of all bit strings with even number of 1’s. Which one of the regular expressions below represents L?

1. (0*10*1)*
2. 0*(10*10*)*
3. 0*(10*1*)*0*
4. 0*1(10*1)*10*

8. Consider the languages L₁ = {0ⁱ1^j | i ≠ j}. L₂ = {0ⁱ1^j | i = j}, L₃ = {0ⁱ1^j |i = 2j + 1}. L₄ = {0ⁱ1^j | i ≠ 2j}. Which one of the following statements is true?

1. Only L₂ is context free
2. Only L₂ and L₃ are context free
3. Only L₁ and L₂ are context free
4. All are context free

9. Let w be any string of length n in {0, 1}*. Let L be the set of all substrings of w. What is the minimum number of states in a non-deterministic finite automaton that accepts L?

1. n-1
2. n
3. n+1
4. 2^n-1

10. Let P be a regular language and Q be a context-free language such that Q ⊆ P (For example let P be the language represented by the regular expression p*q* and Q be {pⁿqⁿ} n ∈ N}, Then which of the following is ALWAYS regular?

1. P ∩ Q
2. P – Q
3. Σ* – P
4. Σ* – Q

11. A deterministic finite automaton (DFA) D with alphabet Σ = {a, b} is given below.

Which of the following finite state machines is a valid minimal DFA which accepts the same language as D?

• A

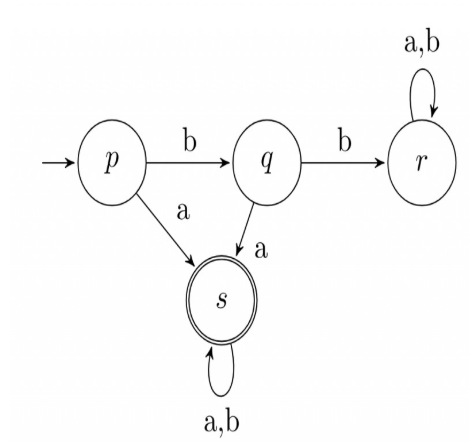
• B

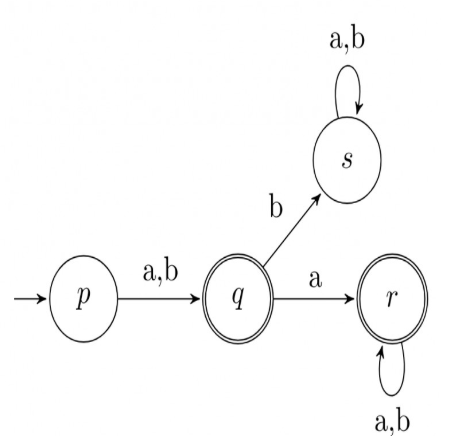
• C

• D

12. Given the language L = {ab, aa, baa}, which of the following strings are in L*?
(i) abaabaaabaa
(ii) aaaabaaaa
(iii) baaaaabaaaab
(iv) baaaaabaa

1. 1, 2 and 3
2. 2, 3 and 4
3. 1, 2 and 4
4. 1, 3 and 4

13. What is the complement of the language accepted by the NFA shown below?
Assume Σ = {a} and ε is the empty string.

1. ∅
2. {ε}
3. a*
4. {a, ε}

14. Consider the set of strings on {0, 1} in which, every substring of 3 symbols has atmost two zeros. For example, 001110 and 011001 are in the language, but 100010 are not. All strings of length less than 3 are also in the language. A partially completed DFA that accepts this language is shown below.
The missing arcs in the DFA are

15. Consider the languages L₁ = Φ and L₂ = {a}. Which one of the following represents L₁L₂* U L₁*?

1. {∈}
2. Φ
3. a*
4. {∈, a}

16. Consider the DFA A given below
Which of the following are FALSE?
i. Complement of L(A) is context-free.
ii. L(A) = L ((11*0 + 0) (0 + 1)*0*1*)
iii. For the language accepted by A, A is the minimal DFA.
iv. A accepts all strings over {0, 1} of length at least 2.

1. 1 and 3 only
2. 2 and 4 only
3. 2 and 3 only
4. 3 and 4 only

17. Consider the finite automaton in the following figure.
What is the set of reachable states for the input string 0011?

1. {q₀, q₁, q₂}
2. {q₀, q₁}
3. {q₀, q₁, q₂,q₃}
4. {q₃}

18. If L₁ = {aⁿ|n ≥ 0} and L₂ = {bⁿ|n ≥ 0}, consider the statements
(i) L₁ . L₂ is a regular language
(ii) L₁ . L₂ = {aⁿ bⁿ|n ≥ 0}
Which one of the following is CORRECT?

1. Only (I)
2. Only (II)
3. Both (I) and (II)
4. Neither (I) nor (II)

19. Let L₁ = {w ∈ {0, 1}*| w has at least as many occurrences of (110)’s as (011)’s}. Let L₂ = {w ∈{0, 1}*|w has at least as many occurrences of (000)’s as (111)’s}. Which one of the following is TRUE?

1. L₁ is regular but not L₂
2. L₂ is regular but not L₁
3. Both L₁ and L₂ are regular
4. Neither L₁ nor L₂ are regular

20. The length of the shortest string NOT in the language (over Σ = {a, b}) of the following regular expression is _.

a*b*(ba)*a*

1. 2
2. 3
3. 4
4. 5

21. Let Σ be finite non-empty alphabet and let 2^Σ* be the power set of Σ^Σ*. Which one of the following is TRUE?
1. Both 2^Σ* and Σ* are countable
2. 2^Σ* is countable and Σ* is uncountable
3. 2^Σ* is uncountable and Σ* is countable
4. Both 2^Σ* and Σ* are uncountable

1. P − 2, Q − 1, R − 3, S − 4
2. P − 1, Q − 3, R − 2, S − 4
3. P − 1, Q − 2, R − 3, S − 4
4. P − 3, Q − 2, R − 1, S − 4

22. Consider the DFAs M and N given above. The number of states in a minimal DFA that accepts the language L(M) ∩ L(N) is _

1. 0
2. 1
3. 2
4. 3

23. The number of states in the minimal deterministic finite automaton corresponding to the regular expression (0 + 1)*(10) is __

1. 0
2. 1
3. 2
4. 3

24. Which of the following languages is/are regular?
L₁: {wxw^R|w₁ x ∈ {a, b}* and |w|, |x| > 0}, w^R is the reverse of string w
L₂: {aⁿb^m|m ≠ n and m, n ≥ 0}
L₃: {a^pb^qc^r| p, q, r ≥ 0}

1. L₁ and L₃ only
2. L₂ only
3. L₂ and L₃ only
4. L₃ only

25. Consider the alphabet Σ = {0, 1}, the null/empty string λ and the sets of strings X₀, X₁ and X₂ generated by the corresponding non-terminals of a regular grammar. X₀, X₁ and X₂ are related as follows
X₀ = 1X₁
X₁ = 0X₁ + 1X₂
X₂ = 0X₁ + {λ}
Which one of the following choices precisely represents the strings in X₀?

1. 10(0* + (10)*)1
2. 10(0* + (10)*)*1
3. 1(0 + 10)*1
4. 10(0 + 10)*1 + 110(0 + 10)*1

26. Let L be the language represented by the regular expression Σ* 0011 Σ* where Σ = {0, 1}. What is the minimum number of states in a DFA that recognizes L’ (complement of L)?

1. 4
2. 5
3. 6
4. 8

27. Which of the following languages is generated by the given grammar?
S →aS | bS | ε

1. {aⁿ b^m | n, m ≥ 0}
2. {w ∈ {a, b} * | w has equal number of a’s and b’s}
3. {aⁿ | n ≥ 0 } U {bⁿ |n ≥ 0 } U {aⁿbⁿ | n ≥ 0}
4. {a, b}*

28. Which of the following decision problems are undecidable?
I. Given NFAs N₁ and N₂, is L (N₁) ∩ L (N₂)= Φ
II. Given a CFG G = (N, ∑, P,S) and a string x ∈ ∑*, does x ∈ L(G)
III. Given CFGs G₁ and G₂, is L(G₁) = L(G₂)
IV Given a TM M, is L(M) = Φ

1. I and IV only
2. II and III only
3. III and IV only
4. II and IV only

29. Which one of the following regular expressions represents the language: the set of all binary strings having two consecutive 0’s and two consecutive 1’s?

1. (0+1)* 0011 (0+1)* + (0+1)* 1100 (0+1)*
2. (0+1)* (00(0+1)*11 + 11 (0+1)*00) (0+1)*
3. (0+1)* 00 (0+1)* + (0+1)* 11 (0+1)*
4. 00 (0+1)* 11 + 11 (0+1)* 00

30. The number of states in the minimum sized DFA that accepts the language defined by the regular expression (0+1)* (0+1) (0+1)* is __ .

1. 0
2. 1
3. 2
4. 3

31. Language L₁ is defined by the grammar: S₁→aS₁b | ∈
Language L₂ is defined by the grammar: S₂→abS₂ | ∈
Consider the following statements:
P : L₁ is regular
Q: L₂ is regular
Which one of the following is TRUE?

1. Both P and Q are true
2. P is true and Q is false
3. P is false and Q is true
4. Both P and Q are false

32. Consider the following two statements:
I. If all states of an NFA are accepting states then the language accepted by the NFA is ∑*.
II. There exists a regular language A such that for all languages B, A ∩ B is regular.
Which one of the following is CORRECT?

1. Only I is true
2. Only II is true
3. Both I and II are true
4. Both I and II are false

33. Consider the language L given by the regular expression (a + b)*b (a + b) over the alphabet {a, b}. The smallest number of states needed in a deterministic finite-state automaton (DFA) accepting L is __.

1. 0
2. 2
3. 4
4. 6

34. The minimum possible number of states of a deterministic finite automaton that accepts the regular language L = {w₁aw₂| w₁, w₂ ∈ {a, b}*, |w₁| = 2, |w₂| ≥ 3} is __.

1. 2
2. 3
3. 8
4. 11

35. Let δ denote the transition function and ^ˆδ denote the extended transition function of the ∈-NFA whose transition table is given below:
Then ^{^}δ (q₂, aba) is

1. Ø
2. {q₀, q₁, q₃}
3. {q₀, q₁, q₂}
4. {q₀, q₂, q₃}

36. Let N be an NFA with n states. Let k be the number of states of a minimal DFA which is equivalent to N. Which one of the following is necessarily true?

1. k ≥ 2ⁿ
2. k ≥ n
3. k ≤ n²
4. k ≤ 2ⁿ

37. Given a language L, define Lⁱ as follows:
L⁰ = {ε}
Lⁱ = L^i-1. L for all i > 0
The order of a language L is defined as the smallest k such that L^k = L^k+1. Consider the language L₁ (over alphabet 0) accepted by the following automaton.The order of L₁ is __.

1. 0
2. 1
3. 2
4. 3

38. Match the following:

1. E − P, F − R, G − Q, H − S
2. E − R, F − P, G − S, H − Q
3. E − R, F − P, G − Q, H − S
4. E − P, F − R, G − S, H − Q

39. Consider the languages L₁, L₂ and L₃ as given below.
L₁ = {0^p 1^q|p, q ∈ N},
L₂ = { 0^p 1^q|p, q ∈ N and p = q} and
L₃ = {0^p 1^q 0^r|p, q, r ∈ N and p = q = r}.
Which of the following statements is NOT TRUE?

1. Push Down Automata (PDA) can be used to recognize L₁ and L₂.
2. L₁ is a regular language.
3. All the three languages are context free
4. Turing machines can be used to recognize all the languages.

40. Which of the following problems are decidable?
(1) Does a given program ever produce an output?
(2) If L is a context-free language, then, is L’ also context-free?
(3) If L is a regular language, then, is L’ also regular?
(4) If L is recursive language, then, is L’ also recursive?

1. 1, 2, 3, 4
2. 1, 2
3. 2, 3, 4
4. 3, 4

41. Consider the following languages.
L₁ = {0^p 1^q 0^r |p, q, r ≥ 0}
L₂ = {0^p 1^q 0^r|p, q, r ≥ 0, p ≠ r}
Which one of the following statements is FALSE?

1. L₂ is context-free
2. L₁ ∩ L₂ is context-free
3. Complement of L₂ is recursive
4. Complement of L₁ is context-free but not regular

42. Which one of the following is TRUE?

1. The language L = {aⁿ bⁿ|n ≥ 0} is regular
2. The language L = {aⁿ|n is prime} is regular
3. The language L = {w|w has 3k + 1b’s for some k ∈N with Σ = {a, b}} is regular
4. The language L = {ww|w∈Σ* with Σ = {0, 1}} is regular.

43. Consider the following languages over the alphabet
Σ = {0, 1, c}.
L₁ = {0ⁿ 1ⁿ|n ≥ 0}
L₂ = {wcw^r|w ∈ {0, 1}*}
L₃ = {ww^r|w ∈{0, 1}*}
Here w^r is the reverse of the string w. Which of these languages are deterministic context-free languages?

1. None of the languages
2. Only L₁
3. Only L₁ and L₂
4. All the three languages

44. Consider the NPDA < Q = {q₀,q₁,q₂}, Σ = {0,1}, Γ = {0,1,⊥}, δ, q₀, ⊥, F = {q₂} >, where (as per usual convention) Q is the set of states, Σ is the input alphabet, Γ is the stack alphabet, δ is the state transition function, q₀ is the initial state, ⊥ is the initial stack symbol, and F is the set of accepting states. The state transition is as follows:
Which one of the following sequences must follow the string 1011 00 so that the overall string is accepted by the automation?

1. 10110
2. 10010
3. 01010
4. 01001

45. Which of the following languages are context-free?
L₁ = {a^mbⁿaⁿb^m | m, n ≥ 1}
L₂ = {a^mbⁿa^mbⁿ | m, n ≥ 1}
L₃ = {a^mbⁿ | m = 2n + 1}

1. L₁ and L₂ only
2. L₁ and L₃ only
3. L₂ and L₃ only
4. L₃ only

46. Consider the following context-free grammars:
G₁ : S → aS|B, B → b|bB
G₂: S → aA|bB, A → aA|B| ε, B |bBε
Which one of the following pairs of languages is generated by G₁ and G₂, respectively?

1. {a^mbⁿ | m > 0 or n > 0} and {a^mbⁿ | m > 0 and n > 0}
2. {a^mbⁿ | m > 0and n > 0} and {a^mbⁿ | m > 0 or n ≥0}
3. {a^mbⁿ | m ≥ 0 or n > 0} and {a^mbⁿ | m > 0 and n > 0}
4. {a^mbⁿ | m ≥ 0 and n > 0} and {a^mbⁿ | m > 0 or n > 0}

47. Consider the transition diagram of a PDA given below with input alphabet ∑ = {a, b} and stack alphabet = {X,Z}. Z is the initial stack symbol. Let L denote the language accepted by the PDA. Which one of the following is TRUE?

1. L = {aⁿ bⁿ| n ≥ 0} and is not accepted by any finite automata.
2. L = {aⁿ | n ≥ 0) ∪ { aⁿ bⁿ | n ≥ 0} and is not accepted by any deterministic PDA.
3. L is not accepted by any Turing machine that halts on every input.
4. L = {aⁿ |n ≥ 0} ∪ {aⁿ bⁿ|n ≥ 0} and is deterministic context-free.

48. Consider the following languages:
L₁ = {aⁿb^mc^n+m : m, n ≥1}
L₂ = {aⁿbⁿc²ⁿ : n ≥ 1}
Which one of the following is TRUE?

1. Both L₁ and L₂ are context-free.
2. L₁ is context-free while L₂ is not context-free
3. L₂ is context-free while L₁ is not context-free.
4. Neither L₁ nor L₂ is context-free.

49. Consider the following context-free grammar over the alphabet Σ = {a, b, c} with S as the start symbol:
S → abScT | abcT
T → bT | b
Which one of the following represents the language generated by the above grammar?

1. {(ab)ⁿ(cb)ⁿ | n ≥ 1}
2. {(ab)ⁿcb^m₁ cb^m₂ ….. cb^m_n | n, m₁, m₂, …… , m_n ≥ 1}
3. {(ab)ⁿ(cb^m)ⁿ | m, n ≥ 1}
4. {(ab)ⁿ(cbⁿ)^m | m, n ≥ 1}

50. If G is a grammar with productions
S → SaS | aSb | bSa | SS |∈
Where S is the start variable, then which one of the following strings is not generated by G?

1. abab
2. aaab
3. abbaa
4. babba

51. Consider the context-free rammers over the alphabet {a, b, c} given below. S and T are non-terminals.
G₁ : S → aSb|T, T → cT|∈
G₂ : S → bSa|T, T → cT|∈
The language L(G₁) ∩ L(G₂) is

1. Finite
2. Not finite but regular
3. Context-Free but not regular
4. Recursive but not context-free.

52. Consider the following languages over the alphabet Σ= {a, b, c}.Let L₁ = {aⁿbⁿc^m| m, n ≥ 0} and L₂ = {a^mbⁿcⁿ| m, n ≥ 0}. Which of the following are context-free languages?
I. L₁ ∪ L₂
II. L₁ ∩ L₂

1. I only
2. II only
3. I and II
4. Neither I nor II

53. Let L₁ L₂ be any two context-free languages and R be any regular language. Then which of the following is/are CORRECT?
I. L₁ ∪ L₂ is context-free.
II. L₁ is context-free.
III. L₁ − R is context-free.
IV. L₁ ∩ L₂ is context-free.

1. I, II and IV only
2. I and III only
3. II and IV only
4. I only

54. Identify the language generated by the following grammar, where S is the start variable.
S → XY
X → aX|a
Y → aYb|∈

1. {a^mbⁿ| m ≥ n, n > 0}
2. {a^mbⁿ| m ≥ n, n ≥ 0}
3. {a^mbⁿ| m >n, n ≥ 0}
4. {a^mbⁿ| m > n, n > 0}

55. Consider the following languages.
L₁ = {a^p | p is a prime number}
L₂ = {aⁿb^mc^2m| n ≥ 0, m ≥ 0}
L₃ = {aⁿbⁿc²ⁿ|n ≥ 0}
L₄ = {aⁿbⁿ | n ≥ 1}
Which of the following are CORRECT?
I. L₁ is context-free but not regular.
II. L₂ is not context-free.
III. L₃ is not context-free but recursive.
IV. L₄ is deterministic and context-free.

1. I, II and IV only
2. II and III only
3. I and IV only
4. III and IV only

56. Consider the following languages:
I. {a^mbⁿc^pd^q | m + p = n + q, where m, n, p, q ≥ 0}
II. {a^mbⁿc^pd^q | m = n and p = q, where m, n, p, q ≥ 0}
III. {a^mbⁿc^pd^q | m = n = p and p ≠ q, where m, n, p, q ≥ 0}
IV. {a^mbⁿc^pd^q | mn = p + q, where m, n, p, q ≥ 0}
Which of the languages above are context-free?

1. I and IV only
2. I and II only
3. II and III only
4. II and IV only

57. For s ∈ (0 + 1)*, let d(s) denote the decimal value of s (e.g., d (101) = 5).
Let L = {s ∈ (0 + 1)*|d(s) mod 5 = 2 and d(s) mod 7 ≠ 4}
Which one of the following statements is true?

1. L is recursively enumerable, but not recursive
2. L is recursive, but not context-free
3. L is context-free, but not regular
4. L is regular

58. Which of the following is true for the language {a^p | p is a prime}?

1. It is not accepted by a Turing Machine
2. It is regular but not context-free
3. It is context-free but not regular
4. It is neither regular nor context-free, but accepted by a Turing machine

59. If L and L’ are recursively enumerable then L is

1. regular
2. context-free
3. context-sensitive
4. recursive

60. Let L = L₁ ∩ L₂, where L₁ and L₂ are languages as defined below:
L₁ = {a^mb^mcaⁿbⁿ | m,n ≥ 0}
L₂ = {aⁱb^jc^k | i,j,k ≥ 0}
Then L is

1. Not recursive
2. Regular
3. Context-free but not regular
4. Recursively enumerable but not context-free.

61. Let L₁ be a recursive language. Let L₂ and L₃ be languages that are recursively enumerable but not recursive. Which of the following statements is not necessarily true?

1. L₂ – L₁ is recursively enumerable
2. L₁ – L₃ is recursively enumerable
3. L₂ ∩ L₁ is recursively enumerable
4. L₂ ∪ L₁ is recursively enumerable

62. Which of the following statements is/are FALSE?
1. For every non-deterministic Turing machine, there exists an equivalent deterministic Turing machine.
2. Turing recognizable languages are closed under union and complementation.
3. Turing decidable languages are closed under intersection and complementation.
4. Turing recognizable languages are closed under union and intersection.

1. 1 and 4 only
2. 1 and 3 only
3. 2 only
4. 3 only

63. Let L be a language and L’ be its complement. Which one of the following is NOT a viable possibility?

1. Neither L nor L’ is recursively enumerable (r. e)
2. One of L and L’ is r.e. but not recursive, the other is not r. e.
3. Both L and L’ are r.e. but not recursive
4. Both L and L’ are recursive

64. Let A ≤_m B denote that language A is mapping reducible (also known as many-to-one reducible) to language B. Which one of the following is FALSE?

1. If A ≤_m B and B is recursive then A is recursive.
2. If A ≤_m B and A is undecidable then B is undecidable.
3. If A ≤_m B and B is recursively enumerable then A is recursively enumerable.
4. If A ≤_m B and B is not recursively enumerable then A is not recursively enumerable.

65. Let <M> be the encoding of a Turing machine as a string over ∑ = {0, 1}. Let L = { <M> |M is a Turing machine that accepts a string of length 2014}. Then, L is

1. Decidable and recursively enumerable
2. Undesirable but recursively enumerable
3. Undesirable and not recursively enumerable
4. Decidable but not recursively enumerable

66. For any two languages L₁ and L₂ such that L₁ is context-free and L₂ is recursively enumerable but not recursive, which of the following is/are necessarily true?
I. L₁‘ (complement of L₁) is recursive
II. L₂‘ (complement of L₂) is recursive
III. L₁‘ is context-free
IV. L₁‘ ∪ L₂ is recursively enumerable

1. I only
2. III only
3. III and IV only
4. I and IV only

67. Consider the following statements.
I. The complement of every Turning decidable language is Turing decidable.
II. There exists some language that is in NP but is not Turing decidable.
III. If L is a language in NP, L is Turing decidable.
Which of the above statements is/are true?

1. Only II
2. Only III
3. Only I and II
4. Only I and III

68. Let X be a recursive language and Y be a recursively enumerable but not recursive language. Let W and Z be two languages such that y’ reduces to W, and Z reduces to x’ (reduction means the standard many one reduction). Which one of the following statements is TRUE?

1. W can be recursively enumerable and Z is recursive.
2. W can be recursive and Z is recursively enumerable.
3. W is not recursively enumerable and Z is recursive.
4. W is not recursively enumerable and Z is not recursive.

69. Consider the following types of languages: L₁: Regular, L₂: Context – free, L₃: Recursive, L₄: Recursively enumerable. Which of the following is /are TRUE?
I. L₃‘ ∪ L₄ is recursively enumerable
II. L₂ ∪ L₃ is recursive
III. L*₁ ∩ L₂ is context – free
IV. L₁ ∪ L₂‘ is context – free

1. I only
2. I and III only
3. I and IV only
4. I, II and III only

70. Consider the following languages.
L₁ = {<M> | M takes at least 2016 steps on some input},
L₂ = {<M> | M takes at least 2016 steps on all inputs} and
L₃ = {<M> | M accepts ε}
where for each Turing machine M, <M> denotes a specific encoding of M. Which one of the following is TRUE?

1. L₁ is recursive and L₂, L₃ are not recursive
2. L₂ is recursive and L₁, L₃ are not recursive
3. L₁, L₂ are recursive L₃ is not recursive
4. L₁, L₂, L₃ are recursive

71. Let A and B be finite alphabets and let # be a symbol outside both A and B. Let f be a total function from A* to B*. We say f is computable if there exists a turning machine M which given an input x in A*, always halts with f(x) on its tape. Let L_f denote the language {x # f(x)| x ∈ A*}. Which of the following statements is true:

1. f is computable if and only if L_f is recursive.
2. f is computable if and only if L_f is recursively enumerable.
3. If f is computable then L_f is recursive, but not conversely.
4. If f is computable then L_f is recursively enumerable, but not conversely.

72. Let L(R) be the language represented by regular expression R. Let L(G) be the language generated by a context-free grammar G. Let L(M) be the language accepted by a Turing machine M. Which of the following decision problems are undecidable?
I. Given a regular expression R and a string w, is w ∈ L(R)
II. Given a context-free grammar G, is L(G) = Ø
III. Given a context-free grammar G, is L(G) = ∑* for some alphabet ∑
IV. Given a Turing machine M and a string w, is w ∈ L(M)

1. I and IV only
2. II and III only
3. II, III and IV only
4. III and IV only

73. The set of all recursively enumerable languages is:

1. Closed under complementation.
2. Closed under intersection.
3. A subset of the set of all recursive languages.
4. An uncountable set.

74. Consider the following problems. L(G) denotes the language generated by a grammar G. L(M) denotes the language accepted by a machine M.
(I) For an unrestricted grammar G and a string w, whether w ∈ L(G)
(II) Given a Turing machine M, whether L(M) is regular
(III)Given two grammars G₁ and G₂, whether L(G₁) = L(G₂)
(IV)Given and NFA N, whether there is a deterministic PDA P such that N and P accept the same language.
Which one of the following statements is correct?

1. Only I and II are undecidable
2. Only III is undecidable
3. Only II and IV are undecidable
4. Only I, II and III are undecidable