Last updated on March 2nd, 2025 at 02:51 pm
Here, we see a Cherry Pickup LeetCode Solution. This Leetcode problem is solved using different approaches in many programming languages, such as C++, Java, JavaScript, Python, etc.
List of all LeetCode Solution
Topics
Level of Question
Hard

Cherry Pickup LeetCode Solution
Table of Contents
1. Problem Statement
You are given an n x n grid representing a field of cherries, each cell is one of three possible integers.
0means the cell is empty, so you can pass through,1means the cell contains a cherry that you can pick up and pass through, or-1means the cell contains a thorn that blocks your way.
Return the maximum number of cherries you can collect by following the rules below:
- Starting at the position
(0, 0)and reaching(n - 1, n - 1)by moving right or down through valid path cells (cells with value0or1). - After reaching
(n - 1, n - 1), returning to(0, 0)by moving left or up through valid path cells. - When passing through a path cell containing a cherry, you pick it up, and the cell becomes an empty cell
0. - If there is no valid path between
(0, 0)and(n - 1, n - 1), then no cherries can be collected.
Example 1:
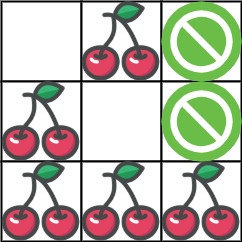
Input: grid = [[0,1,-1],[1,0,-1],[1,1,1]]
Output: 5
Explanation: The player started at (0, 0) and went down, down, right right to reach (2, 2). 4 cherries were picked up during this single trip, and the matrix becomes [[0,1,-1],[0,0,-1],[0,0,0]]. Then, the player went left, up, up, left to return home, picking up one more cherry. The total number of cherries picked up is 5, and this is the maximum possible.
Example 2:
Input: grid = [[1,1,-1],[1,-1,1],[-1,1,1]]
Output: 0
2. Coding Pattern Used in Solution
The coding pattern used in the provided code is “Dynamic Programming on Grids”. This pattern involves solving problems on a 2D grid by breaking them into overlapping subproblems and using memoization or tabulation to optimize the solution. The problem is a variation of the “0/1 Knapsack” pattern, where the goal is to maximize the number of cherries collected while traversing the grid twice (once from top-left to bottom-right and then back).
3. Code Implementation in Different Languages
3.1 Cherry Pickup C++
class Solution {
public:
void cp1(int row, int col, vector<vector<int>>&grid, int ccsf, int &maxcc){
if(row<0 || row>=grid.size() || col<0 || col>= grid[0].size() || grid[row][col]==-1) return;
if(row==grid.size()-1 && col==grid[0].size()-1)
{
bottomToTop(row, col, grid, ccsf, maxcc);
}
int cherries = grid[row][col];
grid[row][col]=0;
cp1(row, col+1, grid, ccsf+cherries, maxcc);
cp1(row+1, col, grid, ccsf+cherries, maxcc);
grid[row][col]=cherries;
}
void bottomToTop(int row, int col, vector<vector<int>>&grid, int ccsf, int &maxcc){
if(row<0 || row>=grid.size() || col<0 || col>= grid[0].size() || grid[row][col]==-1) return;
if(row==0 && col==0)
{
maxcc = max(maxcc, ccsf);
return;
}
int cherries = grid[row][col];
grid[row][col]=0;
bottomToTop(row, col-1, grid, ccsf+cherries, maxcc);
bottomToTop(row-1, col, grid, ccsf+cherries, maxcc);
grid[row][col]=cherries;
}
int cherryPickup(vector<vector<int>>& grid) {
if(grid.size()==1 && grid[0][0]==1) return 1;
int ccsf=0;
int maxcc=0;
cp1(0,0,grid,ccsf,maxcc);
return maxcc;
}
};
3.2 Cherry Pickup Java
class Solution {
public int cherryPickup(int[][] grid) {
int m = grid.length, n = grid[0].length;
maxCherry=0;
rd(0,0,grid,0,m,n);
return maxCherry;
}
int maxCherry;
private void rd(int x, int y, int[][] g, int cpsf, int m, int n){
if(x>=m||y>=n||g[x][y]==-1) return;
if(x==m-1&&y==n-1){
int cherries=g[x][y];
g[x][y]=0;
lu(x,y,g,cpsf+cherries);
g[x][y]=cherries;
return;
}
int cherries = g[x][y];
g[x][y]=0;
rd(x+1,y,g,cpsf+cherries,m,n);
rd(x,y+1,g,cpsf+cherries,m,n);
g[x][y]=cherries;
}
private void lu(int x, int y, int[][] g, int cpsf){
if(x<0||y<0||g[x][y]==-1) return;
if(x==0&&y==0){
maxCherry=Math.max(maxCherry,cpsf);
return;
}
int cherries = g[x][y];
g[x][y]=0;
lu(x-1,y,g,cpsf+cherries);
lu(x,y-1,g,cpsf+cherries);
g[x][y]=cherries;
}
}
3.3 Cherry Pickup JavaScript
var cherryPickup = function(grid) {
let result = 0, N = grid.length, cache = {}, cherries;
const solve = (x1, y1, x2, y2) => {
if(x1 === N -1 && y1 === N-1)
return grid[x1][y1] !== -1 ? grid[x1][y1] : -Infinity;
if(x1 > N -1 || y1 > N-1 || x2 > N-1 || y2 > N-1 || grid[x1][y1] === -1 ||grid[x2][y2] === -1)
return -Infinity;
let lookup_key = `${x1}:${y1}:${x2}:${y2}`;
if(cache[lookup_key]) return cache[lookup_key];
if(x1 === x2 && y1 === y2)
cherries = grid[x1][y1];
else
cherries = grid[x1][y1] + grid[x2][y2];
result = cherries + Math.max(solve(x1 + 1, y1, x2 + 1, y2),
solve(x1, y1 + 1, x2, y2 + 1),
solve(x1 + 1, y1, x2, y2 + 1),
solve(x1, y1 + 1, x2 + 1, y2));
cache[lookup_key] = result;
return result;
};
result = solve(0, 0, 0, 0);
return result > 0 ? result : 0;
};
3.4 Cherry Pickup Python
class Solution(object):
def cherryPickup(self, grid):
m = len(grid)
n = len(grid[0])
self.cherries = 0
self.memo = {}
return max(0, self.dfs(grid, m, n, 0, 0, 0, 0))
def dfs(self, grid, m, n, x1, y1, x2, y2):
if (x1 >= m) or (x2 >= m) or (y1 >= n) or (y2 >= n) or \
grid[x1][y1] == -1 or grid[x2][y2] == -1:
return float('-inf')
if (x1, y1, x2) not in self.memo:
cherries = 0
if grid[x1][y1] == 1:
cherries += 1
if grid[x2][y2] == 1 and x1 != x2:
cherries += 1
if x1 == m-1 and y1 == n-1:
return cherries
cherries += max(
self.dfs(grid, m, n, x1 + 1, y1, x2 + 1, y2),
self.dfs(grid, m, n, x1 + 1, y1, x2, y2 + 1),
self.dfs(grid, m, n, x1, y1 + 1, x2 + 1, y2),
self.dfs(grid, m, n, x1, y1 + 1, x2, y2 + 1),
)
self.memo[(x1, y1, x2)] = cherries
return self.memo[(x1, y1, x2)]
4. Time and Space Complexity
| Time Complexity | Space Complexity | |
| C++ | O(2m + n) | O(m + n) |
| Java | O(2m + n) | O(m + n) |
| JavaScript | O(m² * n²) | O(m² * n²) |
| Python | O(m² * n²) | O(m² * n²) |
- The C++ and Java solutions are brute-force approaches with exponential time complexity.
- The JavaScript and Python solutions use memoization to optimize the recursion, significantly reducing the time complexity to polynomial.
- The problem is a classic example of Dynamic Programming on Grids, where memoization is crucial for efficiency.