Last updated on March 9th, 2025 at 10:24 pm
Here, we see a Maximal Square LeetCode Solution. This Leetcode problem is solved using different approaches in many programming languages, such as C++, Java, JavaScript, Python, etc.
List of all LeetCode Solution
Topics
Companies
Airbnb, Apple, Facebook
Level of Question
Medium

Maximal Square LeetCode Solution
Table of Contents
1. Problem Statement
Given an m x n binary matrix filled with 0’s and 1’s, find the largest square containing only 1’s and return its area.
Example 1: (fig-1) Input: matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]] Output: 4
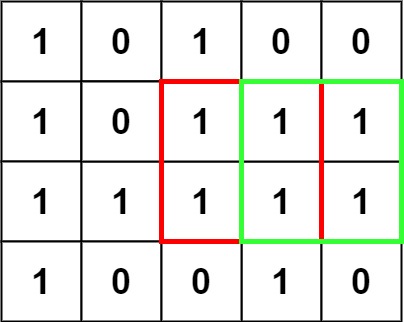
Example 2: (fig-2) Input: matrix = [["0","1"],["1","0"]] Output: 1 Example 3: Input: matrix = [["0"]] Output: 0
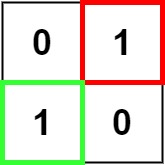
2. Coding Pattern Used in Solution
The coding pattern used in this problem is Dynamic Programming (DP). Specifically, it is a 2D DP problem where the solution builds upon previously computed subproblems to find the maximal square of ‘1’s in a binary matrix.
3. Code Implementation in Different Languages
3.1 Maximal Square C++
class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
if (matrix.empty()) {
return 0;
}
int m = matrix.size(), n = matrix[0].size(), sz = 0;
vector<vector<int>> dp(m, vector<int>(n, 0));
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (!i || !j || matrix[i][j] == '0') {
dp[i][j] = matrix[i][j] - '0';
} else {
dp[i][j] = min(dp[i - 1][j - 1], min(dp[i - 1][j], dp[i][j - 1])) + 1;
}
sz = max(dp[i][j], sz);
}
}
return sz * sz;
}
};
3.2 Maximal Square Java
class Solution {
public int maximalSquare(char[][] matrix) {
if (matrix == null || matrix.length == 0 || matrix[0].length == 0)
return 0;
int max = 0, n = matrix.length, m = matrix[0].length;
int[][] dp = new int[n + 1][m + 1];
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (matrix[i - 1][j - 1] == '1') {
dp[i][j] = Math.min(dp[i - 1][j - 1], Math.min(dp[i - 1][j], dp[i][j - 1])) + 1;
max = Math.max(max, dp[i][j]);
}
}
}
return max * max;
}
}
3.3 Maximal Square JavaScript
var maximalSquare = function(matrix) {
let max = 0
for (let i = 0; i < matrix.length; i++) {
for (let j = 0; j < matrix[0].length; j++) {
if (matrix[i][j] === "0") continue
if(i > 0 && j > 0)
matrix[i][j] = Math.min(matrix[i - 1][j], matrix[i][j - 1], matrix[i - 1][j - 1]) + 1
max = Math.max(matrix[i][j], max)
}
}
return max ** 2
};
3.4 Maximal Square Python
class Solution(object):
def maximalSquare(self, matrix):
if matrix is None or len(matrix) < 1:
return 0
rows = len(matrix)
cols = len(matrix[0])
dp = [[0]*(cols+1) for _ in range(rows+1)]
max_side = 0
for r in range(rows):
for c in range(cols):
if matrix[r][c] == '1':
dp[r+1][c+1] = min(dp[r][c], dp[r+1][c], dp[r][c+1]) + 1
max_side = max(max_side, dp[r+1][c+1])
return max_side * max_side
4. Time and Space Complexity
| Time Complexity | Space Complexity | |
| C++ | O(m * n) | O(m * n) |
| Java | O(m * n) | O(m * n) |
| JavaScript | O(m * n) | O(1) |
| Python | O(m * n) | O(m * n) |
- The JavaScript implementation modifies the input matrix in-place, which reduces the space complexity to O(1). However, this approach may not be suitable if the input matrix cannot be modified.
- The C++, Java, and Python implementations use an additional 2D DP table, resulting in a space complexity of O(m * n).
- All implementations have the same time complexity of O(m * n), as they iterate through the matrix once.