Last updated on March 1st, 2025 at 10:19 pm
Here, we see a Redundant Connection II LeetCode Solution. This Leetcode problem is solved using different approaches in many programming languages, such as C++, Java, JavaScript, Python, etc.
List of all LeetCode Solution
Topics
Depth-First Search, Graph, Tree, Union-Find
Companies
Level of Question
Hard

Redundant Connection II LeetCode Solution
Table of Contents
1. Problem Statement
In this problem, a rooted tree is a directed graph such that, there is exactly one node (the root) for which all other nodes are descendants of this node, plus every node has exactly one parent, except for the root node which has no parents.
The given input is a directed graph that started as a rooted tree with n nodes (with distinct values from 1 to n), with one additional directed edge added. The added edge has two different vertices chosen from 1 to n, and was not an edge that already existed.
The resulting graph is given as a 2D-array of edges. Each element of edges is a pair [ui, vi] that represents a directed edge connecting nodes ui and vi, where ui is a parent of child vi.
Return an edge that can be removed so that the resulting graph is a rooted tree of n nodes. If there are multiple answers, return the answer that occurs last in the given 2D-array.
Example 1:
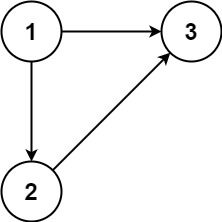
Input: edges = [[1,2],[1,3],[2,3]]
Output: [2,3]
Example 2:
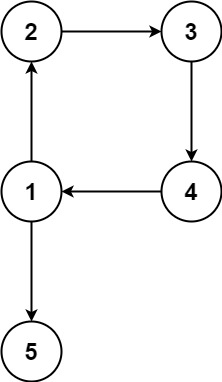
Input: edges = [[1,2],[2,3],[3,4],[4,1],[1,5]]
Output: [4,1]
2. Coding Pattern Used in Solution
The coding pattern used in the provided code is Union-Find (Disjoint Set Union). This pattern is commonly used to solve problems involving connected components, cycles in graphs, and finding redundant connections in a graph. It uses two main operations:
- Find: Determines the root or representative of a set.
- Union: Merges two sets into one.
3. Code Implementation in Different Languages
3.1 Redundant Connection II C++
class DisjointSet
{
int *parent;
int *treeSize;
int n;
public:
DisjointSet(int n)
{
this->n = n;
parent = new int[n];
treeSize = new int[n];
for (int i = 0; i < n; i++)
{
parent[i] = i;
treeSize[i] = 1;
}
}
int find(int x)
{
if (x < 0 || x >= this->n)
return -1;
if (x == parent[x])
return x;
int root = find(parent[x]);
parent[x] = root;
return root;
}
bool connected(int x, int y)
{
return find(x) == find(y);
}
void doUnion(int x, int y)
{
int root1 = find(x);
int root2 = find(y);
if (root1 == root2)
return;
if (this->treeSize[root1] <= this->treeSize[root2])
{
parent[root1] = root2;
this->treeSize[root2] += this->treeSize[root1];
}
else
{
parent[root2] = root1;
this->treeSize[root1] += this->treeSize[root2];
}
}
};
class Solution {
public:
vector<int> findRedundantDirectedConnection(vector<vector<int>>& edges) {
int n = 0;
for(const auto &e : edges)
{
n = max(n, e[0]);
n = max(n, e[1]);
}
DisjointSet ds(n);
vector<int> indeg(n, 0);
int maxIndeg = 0;
for(const auto &e: edges)
{
int v = e[1] - 1;
indeg[v]++;
maxIndeg = max(maxIndeg, indeg[v]);
}
if(maxIndeg == 1)
{
vector<int> res = {-1,-1};
for(const auto &e : edges)
{
int u = e[0] - 1;
int v = e[1] - 1;
if(ds.connected(u, v))
res = {u+1, v+1};
ds.doUnion(u, v);
}
return res;
}
else
{
vector<int> e1 = {-1, -1};
vector<int> e2 = {-1, -1};
for(const auto &e : edges)
{
int u = e[0] - 1;
int v = e[1] - 1;
if(indeg[v] == 2)
{
if(e1 == vector<int>({-1,-1}) )
e1 = {u,v};
else
e2 = {u,v};
}
}
for(const auto &e : edges)
{
int u = e[0] - 1;
int v = e[1] - 1;
if(e2 != vector<int>({u,v}) )
ds.doUnion(u, v);
}
if(ds.connected(e2[0], e2[1]))
return {e2[0] + 1, e2[1] + 1};
else
return {e1[0] + 1, e1[1] + 1};
}
}
};
3.2 Redundant Connection II Java
class Solution {
public int[] findRedundantDirectedConnection(int[][] edges) {
int[]inDegree = new int[edges.length+1];
Arrays.fill(inDegree, -1);
int bl1 = -1, bl2 = -1;
for(int i=0; i<edges.length; i++){
int u = edges[i][0];
int v = edges[i][1];
if(inDegree[v] == -1){
inDegree[v] = i;
} else {
bl1 = i;
bl2 = inDegree[v];
break;
}
}
int[]parent = new int[edges.length+1];
int[]rank = new int[edges.length+1];
for(int i=0; i<parent.length; i++) parent[i] = i;
for(int i=0; i<edges.length; i++){
if(i == bl1) continue;
int[]edge = edges[i];
boolean bool = union(edge[0], edge[1], parent, rank);
if(bool){
if(bl1 == -1){
return edge;
} else{
return edges[bl2];
}
}
}
return edges[bl1];
}
public int find(int x, int[]parent){
if(x == parent[x]) return x;
else return find(parent[x], parent);
}
public boolean union(int s1, int s2, int[]parent, int[]rank){
int s1lead = find(s1, parent);
int s2lead = find(s2, parent);
if(s1lead != s2lead){
if(rank[s1lead] > rank[s2lead]){
parent[s2lead] = s1lead;
} else if(rank[s2lead] > rank[s1lead]){
parent[s1lead] = s2lead;
} else{
parent[s2lead] = s1lead;
rank[s1lead]++;
}
return false;
} else return true;
}
}
3.3 Redundant Connection II JavaScript
var findRedundantDirectedConnection = function (edges) {
let n = edges.length;
let parent = Array(n + 1).fill(0);
let first = second = [];
for (let edge of edges) {
if (parent[edge[1]] === 0) {
parent[edge[1]] = edge[0];
} else {
first = [parent[edge[1]], edge[1]];
second = [...edge];
edge[1] = 0;
}
}
for (let i = 0; i <= n; ++i) parent[i] = i;
for (let edge of edges) {
if (edge[1] === 0) continue;
let [x, y] = [find(parent, edge[0]), find(parent, edge[1])];
if (x === y) return first.length === 0 ? edge : first;
parent[x] = y;
}
return second;
};
function find(parent, x) {
return x === parent[x] ? x : find(parent, parent[x]);
}
3.4 Redundant Connection II Python
class Solution(object):
def findRedundantDirectedConnection(self, edges):
n = len(edges)
parent = dict(zip(range(1,n+1), range(1,n+1)))
last_cycle_edge = candidate_edge = candidate = None
def root(v):
while parent[v] != v:
v = parent[v]
return v
for e in edges:
v, w = e
if parent[w] != w:
candidate_edge, candidate = e, w
continue
if root(v) == w:
last_cycle_edge = e
continue
parent[w], n = v, n-1
return [parent[candidate], candidate] if n > 1 else (candidate_edge or last_cycle_edge)
4. Time and Space Complexity
| Time Complexity | Space Complexity | |
| C++ | O(E * α(V)) | O(V) |
| Java | O(E * α(V)) | O(V) |
| JavaScript | O(E * α(V)) | O(V) |
| Python | O(E * α(V)) | O(V) |
where,E is the number of edges.V is the number of vertices.
α is the inverse Ackermann function, which grows extremely slowly and is considered nearly constant.
- The code uses the Union-Find (Disjoint Set Union) pattern to efficiently detect and resolve redundant edges in a directed graph.
- It leverages path compression and rank/size optimization to ensure near-constant time for union and find operations.
- The overall time complexity is O(E * α(V)), and the space complexity is O(V) across all implementations.