Last updated on March 1st, 2025 at 09:56 pm
Here, we see a Perfect Rectangle LeetCode Solution. This Leetcode problem is solved using different approaches in many programming languages, such as C++, Java, JavaScript, Python, etc.
List of all LeetCode Solution
Topics
Line-Sweep
Companies
Level of Question
Hard

Perfect Rectangle LeetCode Solution
Table of Contents
1. Problem Statement
Given an array rectangles where rectangles[i] = [xi, yi, ai, bi] represents an axis-aligned rectangle. The bottom-left point of the rectangle is (xi, yi) and the top-right point of it is (ai, bi).
Return true if all the rectangles together form an exact cover of a rectangular region.
Example 1:
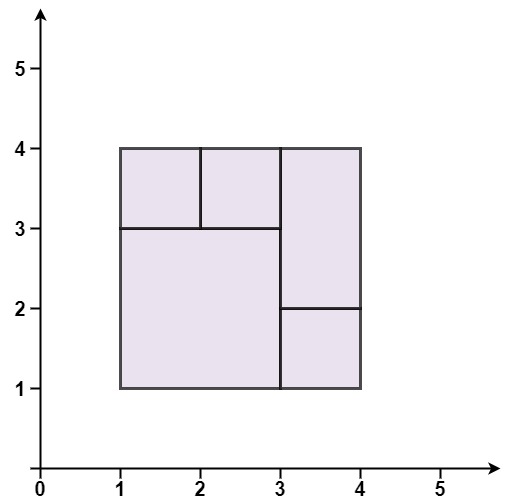
Input: rectangles = [[1,1,3,3],[3,1,4,2],[3,2,4,4],[1,3,2,4],[2,3,3,4]]
Output: true
Explanation: All 5 rectangles together form an exact cover of a rectangular region.
Example 2:
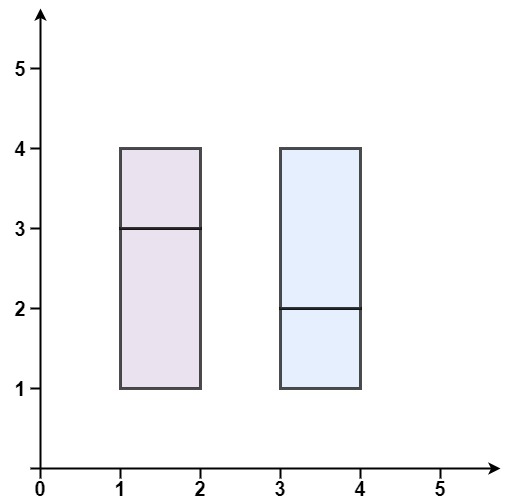
Input: rectangles = [[1,1,2,3],[1,3,2,4],[3,1,4,2],[3,2,4,4]]
Output: false
Explanation: Because there is a gap between the two rectangular regions.
Example 3:
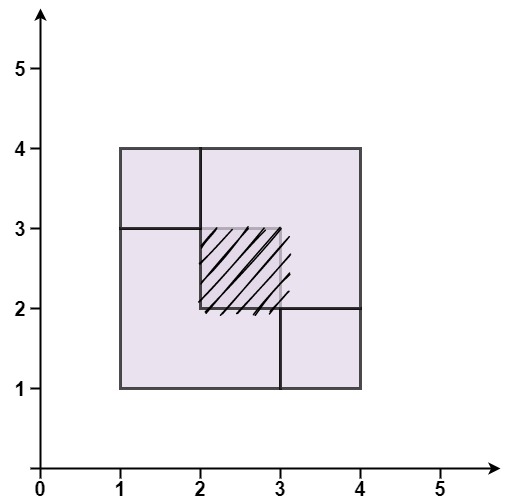
Input: rectangles = [[1,1,3,3],[3,1,4,2],[1,3,2,4],[2,2,4,4]]
Output: false
Explanation: Because two of the rectangles overlap with each other.
2. Coding Pattern Used in Solution
The coding pattern used in this problem is “Geometry and Hashing”. The solution uses hashing (via map, set, or similar data structures) to track the corners of rectangles and validate the conditions for forming a perfect rectangle.
3. Code Implementation in Different Languages
3.1 Perfect Rectangle C++
class Solution {
public:
bool isRectangleCover(vector<vector<int>>& rectangles) {
int n = rectangles.size();
if (n == 1) return true;
map<pair<int, int>, int> pointCounts;
for (auto& rect : rectangles) {
pointCounts[{rect[0], rect[1]}]++;
pointCounts[{rect[2], rect[3]}]++;
pointCounts[{rect[0], rect[3]}]--;
pointCounts[{rect[2], rect[1]}]--;
}
int numMarks = 0;
for (auto it = pointCounts.begin(); it != pointCounts.end(); it++) {
if (it->second != 0) {
if (abs(it->second) != 1) return false;
numMarks++;
}
}
return numMarks == 4;
}
};
3.2 Perfect Rectangle Java
class Solution {
public boolean isRectangleCover(int[][] rectangles) {
if (rectangles.length == 0 || rectangles[0].length == 0) return false;
Set<String> points = new HashSet<String>();
int area = 0;
int minX = Integer.MAX_VALUE;
int minY = Integer.MAX_VALUE;
int maxA = Integer.MIN_VALUE;
int maxB = Integer.MIN_VALUE;
for (int[] r : rectangles){
int x = r[0];
int y = r[1];
int a = r[2];
int b = r[3];
area += (x-a) * (y-b);
minX = Math.min(minX, x);
minY = Math.min(minY, y);
maxA = Math.max(maxA, a);
maxB = Math.max(maxB, b);
String bottomLeft = getHash(x,y);
String topLeft = getHash(x,b);
String bottomRight = getHash(a,y);
String topRight = getHash(a,b);
checkInSet(points, bottomLeft);
checkInSet(points, topLeft);
checkInSet(points, bottomRight);
checkInSet(points, topRight);
}
String fullBottomLeft = getHash(minX,minY);
String fullTopLeft = getHash(minX,maxB);
String fullBottomRight = getHash(maxA,minY);
String fullTopRight = getHash(maxA,maxB);
if (points.size() != 4 || !points.contains(fullBottomLeft)
|| !points.contains(fullTopLeft) || !points.contains(fullBottomRight) || !points.contains(fullTopRight)) return false;
int fullArea = (minX-maxA) * (minY-maxB);
return area == fullArea;
}
private void checkInSet(Set<String> points, String hash){
if (!points.contains(hash)) points.add(hash);
else points.remove(hash);
}
private String getHash(int x, int y){
return x + ":" + y;
}
}
3.3 Perfect Rectangle JavaScript
var isRectangleCover = function(rectangles) {
let corners = new Set();
let l = Infinity, r = 0, t = 0, dummy = Infinity, area = 0;
function key(x, y){
return x + (y === 0 ? 0 : .1 / y);
}
function track(x, y){
let n = key(x, y);
if(corners.has(n)) corners.delete(n);
else corners.add(n);
}
for(let i = 0; i < rectangles.length; i++){
let[x1, y1, x2, y2] = rectangles[i];
l = Math.min(l, x1);
t = Math.max(t, y2);
r = Math.max(r, x2);
dummy = Math.min(dummy, y1);
area += (x2 - x1) * (y2 - y1);
track(x1, y1);
track(x1, y2);
track(x2, y1);
track(x2, y2);
}
return (
area === (t - dummy) * (r - l)
&& 4 === corners.size
&& corners.has(key(l, dummy))
&& corners.has(key(r, dummy))
&& corners.has(key(l, t))
&& corners.has(key(r, t))
)
};
3.4 Perfect Rectangle Python
class Solution(object):
def isRectangleCover(self, rectangles):
area = 0
corners = set()
for x1, y1, x2, y2 in rectangles:
area += (x2 - x1) * (y2 - y1)
for corner in [(x1, y1), (x1, y2), (x2, y1), (x2, y2)]:
if corner in corners:
corners.remove(corner)
else:
corners.add(corner)
if len(corners) != 4:
return False
x1, y1 = float("inf"), float("inf")
x2, y2 = float("-inf"), float("-inf")
for x, y in corners:
x1 = min(x1, x)
y1 = min(y1, y)
x2 = max(x2, x)
y2 = max(y2, y)
union_area = (x2 - x1) * (y2 - y1)
if area != union_area:
return False
return area == (x2 - x1) * (y2 - y1)
4. Time and Space Complexity
| Time Complexity | Space Complexity | |
| C++ | O(n) | O(n) |
| Java | O(n) | O(n) |
| JavaScript | O(n) | O(n) |
| Python | O(n) | O(n) |